ГДЗ по Математике 5 Класс Номер 688 Дорофеев, Шарыгин, Суворова — Подробные Ответы

Задача

а) Начертите треугольник, один из углов которого прямой. Измерьте и запишите длины сторон треугольника. Что больше: самая большая сторона треугольника или сумма двух других его сторон? Найдите периметр треугольника.

б) Начертите треугольник, один из углов которого тупой, и выполните те же задания, что и в пункте «а».

Краткий ответ:

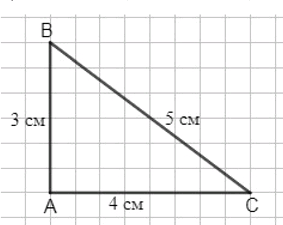
а) Прямоугольный треугольник:

Стороны: 3, 4, 5.
Самая длинная сторона меньше суммы других.
Периметр: 12.

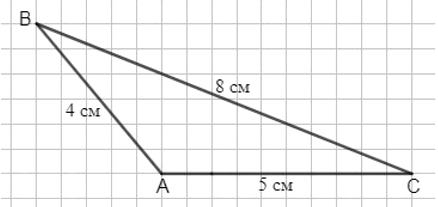
б) Тупоугольный треугольник:

Стороны: 4, 5, 8.
Самая длинная сторона меньше суммы других.
Периметр: 17.

Подробный ответ:

а) Прямоугольный треугольник

Построение:

Начертите треугольник с одним прямым углом (90 градусов). Используйте линейку и угольник для точности.

Измерение сторон:

Измерьте длины катетов и гипотенузы. Предположим, что получились следующие длины: 3, 4 и 5.

Сравнение сторон:

Гипотенуза (5) является самой длинной стороной.

Сумма двух других сторон: 3 + 4 = 7.

Сравнение: гипотенуза меньше суммы катетов (5 < 7).

Периметр:

Периметр треугольника: 3 + 4 + 5 = 12.

Вывод для а):

Гипотенуза меньше суммы двух других сторон.

Периметр треугольника: 12.

б) Тупоугольный треугольник

Построение:

Начертите треугольник с одним тупым углом (больше 90 градусов). Используйте транспортир для точности.

Измерение сторон:

Измерьте длины сторон. Предположим, что получились следующие длины: 4, 5 и 8, где 8 — сторона напротив тупого угла.

Сравнение сторон:

Сторона 8 является самой длинной.

Сумма двух других сторон: 4 + 5 = 9.

Сравнение: самая длинная сторона меньше суммы двух других (8 < 9).

Периметр:

Периметр треугольника: 4 + 5 + 8 = 17.

Вывод для б):

Самая длинная сторона меньше суммы двух других сторон.

Периметр треугольника: 17.

Оцени решение