ГДЗ по Математике 5 Класс Номер 621 Дорофеев, Шарыгин, Суворова — Подробные Ответы
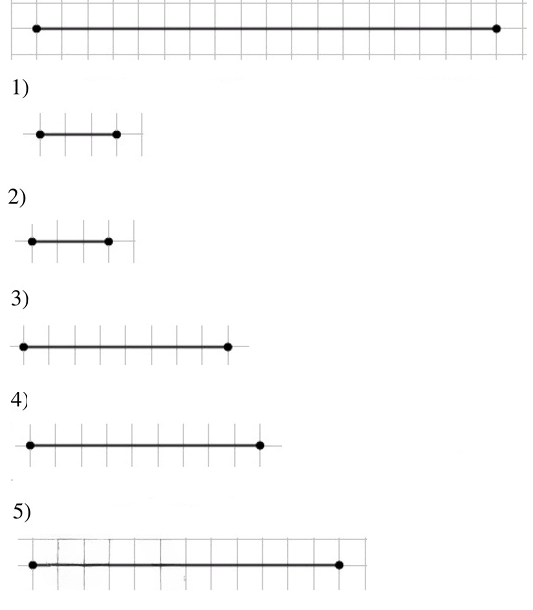
Рассуждаем. Начертите отрезок длиной 18 клеток. Начертите отрезки, равные 3/18, 1/6, 4/9, 1/2 данного отрезка.
Будем рассуждать так: для того чтобы построить отрезок, равный 3/18 данного отрезка, выясним, чему равна длина одной восемнадцатой доли отрезка, а затем – трёх восемнадцатых:
18 : 18 = 1 (клетка), 1 ⋅ 3 = 3 (клетки).
Теперь можно построить требуемый отрезок. Рассуждая так же, постройте и остальные отрезки.
Отрезок длиной 18 клеток:
- Длина одной восемнадцатой доли отрезка равна:
18 : 18 = 1 (клетке).
Значит, длина 3/18 равна:
1 × 3 = 3 (клеткам). - Длина одной шестой доли отрезка равна:
18 : 6 = 3 (клеткам). - Длина одной девятой доли отрезка равна:
18 : 9 = 2 (клеткам).
Значит, длина 4/9 равна:
2 × 4 = 8 (клеткам). - Длина одной второй доли отрезка равна:
18 : 2 = 9 (клеткам). - Длина одной третьей доли отрезка равна:
18 : 3 = 6 (клеткам).
Значит, длина 2/3 равна:
6 × 2 = 12 (клеткам).
1) Отрезок длиной 18 клеток:
Начнем с нахождения длины одной восемнадцатой доли отрезка. Это делается путем деления всей длины отрезка на 18.
18 : 18 = 1 клетка. Это означает, что одна восемнадцатая часть отрезка равна 1 клетке.
Чтобы найти длину трех восемнадцатых долей, умножаем результат на 3: 1 × 3 = 3 клетки.
Построим отрезок длиной 3 клетки.
2) Длина одной шестой доли отрезка:
Делим длину отрезка на 6: 18 : 6 = 3 клетки.
Это означает, что одна шестая часть отрезка равна 3 клеткам.
3) Длина одной девятой доли отрезка:
Делим длину отрезка на 9: 18 : 9 = 2 клетки.
Чтобы найти длину четырех девятых долей, умножаем результат на 4: 2 × 4 = 8 клеток.
Построим отрезок длиной 8 клеток.
4) Длина одной второй доли отрезка:
Делим длину отрезка на 2: 18 : 2 = 9 клеток.
Это означает, что одна вторая часть отрезка равна 9 клеткам.
5) Длина одной третьей доли отрезка:
Делим длину отрезка на 3: 18 : 3 = 6 клеток.
Чтобы найти длину двух третьих долей, умножаем результат на 2: 6 × 2 = 12 клеток.
Построим отрезок длиной 12 клеток.
