Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 598 Дорофеев, Шарыгин, Суворова — Подробные Ответы
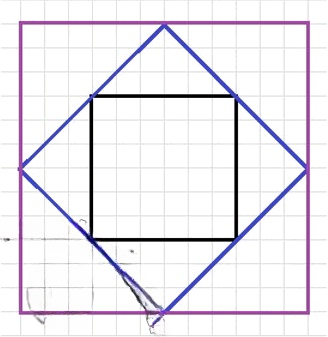
1) Закрашенная часть квадрата тоже квадрат (рис. 7.35). Убедитесь в этом, выполнив необходимые измерения. Во сколько раз площадь закрашенного квадрата меньше площади большого квадрата?
Подсказка. Скопируйте рисунок на лист бумаги в клетку, вырежите квадрат и перегните прямо угольные треугольники к центру по сторонам закрашенного квадрата.
2) Площадь красного квадрата (рис. 7.36) равна 1 кв. ед. Чему равна площадь чёрного квадрата?
3) Пусть площадь чёрного квадрата (см. рис. 7.36) равна 2 кв. ед. Начертите квадрат, площадь которого равна 8 кв. ед.
1) Закрашенный квадрат является квадратом, потому что: стороны закрашенного квадрата равны, а все углы прямые.
Площадь закрашенного квадрата в 2 раза меньше площади большого квадрата. Ответ: в 2 раза.
2) Площадь желтого квадрата равна 1 · 2 = 2 кв. ед.
Площадь зеленого квадрата равна 2 · 2 = 4 кв. ед.
Площадь голубого квадрата равна 4 · 2 = 8 кв. ед.
Площадь синего квадрата равна 8 · 2 = 16 кв. ед.
Площадь фиолетового квадрата равна 16 · 2 = 32 кв. ед.
Площадь черного квадрата равна 32 · 2 = 64 кв. ед.
Ответ: 64 кв. ед.
3) Площадь черного квадрата 2 кв. ед.
Площадь синего квадрата 2 · 2 = 4 кв. ед.
Площадь фиолетового квадрата 4 · 2 = 8 кв. ед.
1) Закрашенный квадрат:
Закрашенный квадрат является квадратом, потому что его стороны равны, а углы прямые.
Площадь закрашенного квадрата в 2 раза меньше площади большого квадрата. Это можно проверить, если сложить треугольники внутрь закрашенного квадрата. Таким образом, площадь закрашенного квадрата равна половине площади большого квадрата.
2) Площадь красного квадрата:
Площадь красного квадрата равна 1 кв. ед.
Следовательно, если стороны увеличиваются в 2 раза, то площадь увеличивается в 4 раза.
Площадь следующего (желтого) квадрата: 1 * 2 = 2 кв. ед.
Площадь зеленого квадрата: 2 * 2 = 4 кв. ед.
Площадь голубого квадрата: 4 * 2 = 8 кв. ед.
Площадь синего квадрата: 8 * 2 = 16 кв. ед.
Площадь фиолетового квадрата: 16 * 2 = 32 кв. ед.
Площадь черного квадрата: 32 * 2 = 64 кв. ед.
3) Площадь черного квадрата:
Если площадь черного квадрата равна 2 кв. ед., то для получения квадрата с площадью 8 кв. ед. нужно увеличить сторону в корне из раз.
Это соответствует увеличению площади в 4 раза, так как 2 * 4 = 8 кв. ед.
Математика
