ГДЗ по Математике 5 Класс Номер 590 Дорофеев, Шарыгин, Суворова — Подробные Ответы

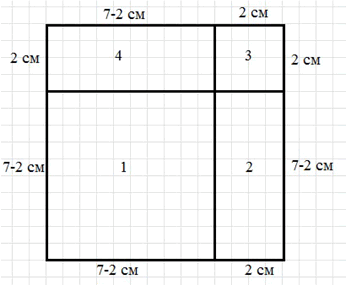
Сторона большого квадрата равна 7 см (рис. 7.34). Найдите площадь каждой его части.

S1 = (7 — 2) × (7 — 2) = 5 × 5 = 25 см².
S2 = S4 = 2 × (7 — 2) = 2 × 5 = 10 см².
S3 = 2 × 2 = 4 см².

Ответ: 25 см²; 10 см²; 10 см²; 4 см².

Анализ фигуры:

У нас есть большой квадрат со стороной 7 см, разделенный на четыре части.

Эти части обозначены как S1, S2, S3, и S4.

Вычисление площади каждой части:

Часть S1:

Это квадрат со стороной 5 см (7 см — 2 см).

Площадь S1 = 5 см × 5 см = 25 см².

Части S2 и S4:

Это прямоугольники с размерами 2 см × 5 см.

Площадь S2 = 2 см × 5 см = 10 см².

Площадь S4 = 2 см × 5 см = 10 см² (аналогично S2).

Часть S3:

Это квадрат со стороной 2 см.

Площадь S3 = 2 см × 2 см = 4 см².

Проверка:

Сумма площадей всех частей должна равняться площади большого квадрата.

25 см² + 10 см² + 10 см² + 4 см² = 49 см².

Площадь большого квадрата: 7 см × 7 см = 49 см².

Ответ: 25 см²; 10 см²; 10 см²; 4 см².