Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 569 Дорофеев, Шарыгин, Суворова — Подробные Ответы
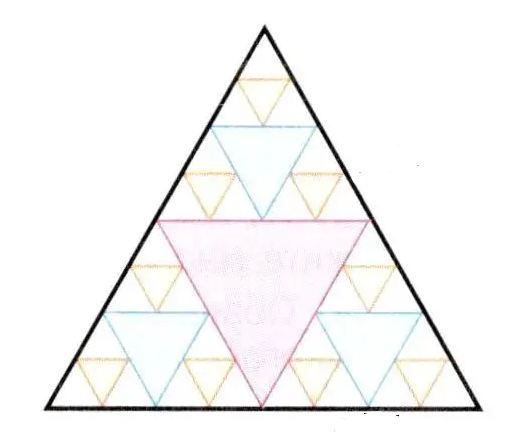
Треугольник, изображённый на рисунке 7.27, носит название «треугольник Серпинского» в честь создавшего его польского математика.
1) Рассмотрите его и ответьте на вопросы:
а) каков вид треугольников;
б) есть ли среди них равные (приведите пример);
в) во сколько раз сторона красного треугольника меньше стороны большого треугольника? сторона синего треугольника меньше стороны красного? сторона жёлтого меньше стороны синего?
2) Подсчитайте число всех треугольников на рисунке.
3) Расскажите алгоритм построения треугольника Серпинского.
Подсказка. Равные треугольники считайте отдельно.
1) а) Треугольники равносторонние. б) Равные треугольники: все желтые; все синие. в) Сторона красного треугольника меньше стороны большого треугольника в 2 раза; сторона синего треугольника меньше стороны красного треугольника в 2 раза; сторона желтого треугольника меньше стороны синего треугольника в 2 раза.
2) Всего на рисунке 14 треугольников:
- 9 желтых;
- 3 синих;
- 1 розовый;
- 1 большой;
- итого: 9 + 3 + 1 + 1 = 14.
3) Алгоритм построения треугольника Серпинского:
- рисуем большой треугольник;
- делим его на четыре равных треугольника;
- далее полученные треугольники делим еще на четыре равных треугольника;
- новые полученные треугольники снова делим на четыре равных треугольника и т. д.
1) Рассмотрение треугольников
а) Вид треугольников:
Все треугольники равносторонние, то есть у них все стороны и углы равны.
б) Равные треугольники:
Все желтые треугольники равны между собой.
Все синие треугольники равны между собой.
в) Сравнение сторон:
Сторона красного треугольника меньше стороны большого треугольника в 2 раза.
Сторона синего треугольника меньше стороны красного треугольника в 2 раза.
Сторона желтого треугольника меньше стороны синего треугольника в 2 раза.
2) Подсчет треугольников
Всего на рисунке 14 треугольников:
9 желтых треугольников
3 синих треугольника
1 розовый треугольник
1 большой треугольник
Итого: 9 + 3 + 1 + 1 = 14 треугольников.
3) Алгоритм построения треугольника Серпинского
Рисуем большой треугольник.
Делим его на четыре равных треугольника:
На каждом этапе деления треугольник делится на три меньших треугольника, оставляя центральный пустым.
Далее полученные треугольники делим еще на четыре равных треугольника:
Процесс повторяется для каждого из оставшихся треугольников.
Продолжаем деление:
Каждый новый треугольник снова делится на четыре равных треугольника, и так далее.
Математика
