Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
ГДЗ по Математике 5 Класс Номер 560 Дорофеев, Шарыгин, Суворова — Подробные Ответы
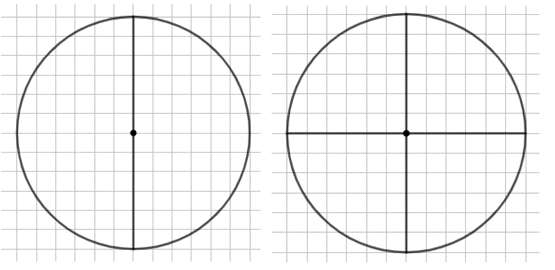
1) Начертите в тетради круг и разделите его отрезком на две равные части. Как называется этот отрезок? Разделите круг на четыре равные части.
2) Как путём перегибания можно найти центр круга?
1) Отрезок, который делит круг на две равные части — это диаметр.
2) Чтобы найти центр круга путем перегибаний, надо сложить круг пополам, а затем полученный полукруг сложить пополам. Точка пересечения сгибов является центром круга.
Разделение круга на две равные части:
Начертите круг в тетради.
Проведите отрезок через центр круга, соединяющий две противоположные точки окружности.
Этот отрезок называется диаметром.
Диаметр делит круг на две равные части.
Разделение круга на четыре равные части:
После проведения первого диаметра, проведите еще один диаметр, перпендикулярный первому.
Теперь у вас есть два диаметра, пересекающихся в центре круга.
Эти диаметры делят круг на четыре равные части.
Нахождение центра круга путем перегибания:
Вырежьте круг из бумаги.
Сложите круг пополам, чтобы получить полукруг.
Разверните и снова сложите пополам, но в другой плоскости.
Точка пересечения сгибов будет центром круга.
