Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 559 Дорофеев, Шарыгин, Суворова — Подробные Ответы
1) Начертите прямоугольник, обозначьте его и проведите одну диагональ. Диагональ разделила прямо угольник на два равных треугольника. Покажите на чертеже и назовите их равные стороны и равные углы.
2) Возьмите вырезанный из бумаги прямоугольник и разрежьте его по диагонали. Сложите из получившихся равных треугольников равнобедренный треугольник.
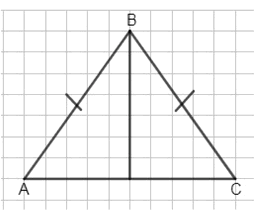
3) Равнобедренный треугольник АВС (рис. 7.21) разрезали по отрезку ВО. Каков вид получившихся треугольников? Из этих треугольников сложили прямоугольник. Нарисуйте его. Какой из сторон треугольника равна диагональ прямоугольника?
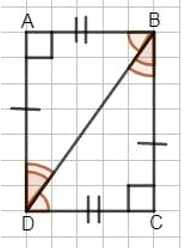
1) Прямоугольник ABCD. Диагональ BD.
AD = BC; AB = CD; ∠A = ∠C;
∠ABD = ∠CDB; ∠ADB = ∠CBD.
2) Равнобедренный треугольник из получившихся равных треугольников:
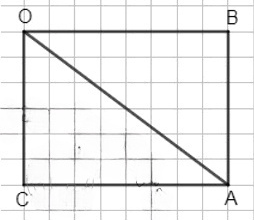
3) Получилось два равных прямоугольных треугольника. Диагональ прямоугольника равна сторонам треугольника AB и BC, то есть, OA = AB = BC.
1) Построение прямоугольника и диагонали:
Начертите прямоугольник ABCD.
Проведите диагональ BD.
Диагональ BD разделяет прямоугольник на два равных треугольника: ABD и BCD.
Так как ABCD — это прямоугольник, то противоположные стороны равны: AD = BC и AB = CD.
Углы при основании диагонали равны: ∠ABD = ∠CDB и ∠ADB = ∠CBD, так как диагональ делит углы пополам.
2) Создание равнобедренного треугольника:
Возьмите бумажный прямоугольник и разрежьте его по диагонали BD.
Получатся два равных треугольника ABD и BCD.
Сложите их так, чтобы стороны AB и BC совпали, образуя равнобедренный треугольник.
3) Анализ равнобедренного треугольника:
Дано, что равнобедренный треугольник ABC разрезан по отрезку BO.
Получившиеся треугольники — это два равных прямоугольных треугольника.
Из этих треугольников можно сложить прямоугольник, где диагональ равна сторонам треугольника AB и BC.
Таким образом, в прямоугольнике OA = AB = BC.
Математика
