
Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
ГДЗ по Математике 5 Класс Номер 530 Дорофеев, Шарыгин, Суворова — Подробные Ответы
Строим по алгоритму.
1) Постройте на нелинованной бумаге равнобедренный треугольник ABC по следующему алгоритму:
-Начертите отрезок АС – основание треугольника.
-Проведите циркулем две равные окружности с центрами в точках А и С так, чтобы окружности пересекались; одну из точек пересечения обозначьте буквой В.
-Проведите отрезки АВ и ВС.
2) Постройте равнобедренный треугольник, у которого:
а) основание равно 5 см, а боковые стороны – 4 см;
б) основание равно 6 см, а боковые стороны – 3 см 5 мм.
- Пусть AC = 5 см.
Окружности с центрами в точках A и C радиусом 3 см 5 мм. - а) AC = 5 см; AB = BC = 4 см.
б) AC = 6 см; AB = BC = 3 см 5 мм.
1) Построение равнобедренного треугольника ABC
Начертите отрезок AC:
На нелинованной бумаге начертите отрезок AC длиной 5 см. Это будет основание треугольника.
Проведите две окружности:
Центр первой окружности находится в точке A, радиус — 3 см 5 мм.
Центр второй окружности находится в точке C, радиус — 3 см 5 мм.
Эти окружности должны пересекаться.
Обозначьте точку пересечения:
Одну из точек пересечения окружностей обозначьте как точку B.
Проведите отрезки AB и BC:
Соедините точки A и B, а также точки B и C отрезками. Получившийся треугольник ABC будет равнобедренным.
2) Построение равнобедренного треугольника с заданными сторонами
а) Основание 5 см, боковые стороны 4 см
Начертите отрезок AC:
Начертите отрезок AC длиной 5 см.
Проведите две окружности:
Центр первой окружности в точке A, радиус — 4 см.
Центр второй окружности в точке C, радиус — 4 см.
Окружности должны пересекаться.
Обозначьте точку пересечения:
Обозначьте одну из точек пересечения как точку B.
Проведите отрезки AB и BC:
Соедините точки A и B, а также B и C.
б) Основание 6 см, боковые стороны 3 см 5 мм
Начертите отрезок AC:
Начертите отрезок AC длиной 6 см.
Проведите две окружности:
Центр первой окружности в точке A, радиус — 3 см 5 мм.
Центр второй окружности в точке C, радиус — 3 см 5 мм.
Окружности должны пересекаться.
Обозначьте точку пересечения:
Обозначьте одну из точек пересечения как точку B.
Проведите отрезки AB и BC:
Соедините точки A и B, а также B и C.
Пусть AC = 5 см. Окружности с центрами в точках A и C радиусом 3 см 5 мм.
а) AC = 5 см; AB = BC = 4 см.
б) AC = 6 см; AB = BC = 3 см 5 мм.


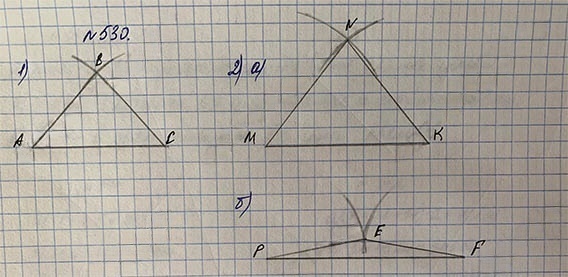


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!