ГДЗ по Математике 5 Класс Номер 523 Дорофеев, Шарыгин, Суворова — Подробные Ответы

1) Треугольник АВС (рис. 7.5) равнобедренный. Назовите его:
а) основание;
б) боковые стороны;
в) углы при основании;
г) угол, противолежащий основанию.

2) Найдите на рисунке 7.6 равнобедренные треугольники и скопируйте их в тетрадь. Укажите боковые стороны и основание каждого из треугольников. Измерьте и запишите длины сторон и величины углов треугольника

1) AB = AC. а) Основание — BC.

б) Боковые стороны — AB и AC.

в) Углы при основании — ∠B и ∠C.

г) Угол, противолежащий основанию — ∠A.

2) Равнобедренные треугольники: NOP; DEF; ABC.

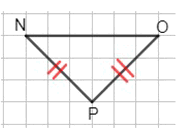
Треугольник NOP:

NO = 3 см — основание;

NP = OP = 2,1 см.

∠N = ∠O = 45°;

∠P = 90°.

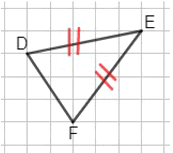
Треугольник DEF:

DF = 1,8 см — основание;

DE = EF = 2,5 см.

∠D = ∠F = 70°;

∠E = 40°.

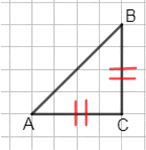
Треугольник ABC:

AB = 2,9 см — основание;

AC = BC = 2 см.

∠A = ∠B = 45°;

∠C = 90°.

1) Понимание равнобедренного треугольника

Равнобедренный треугольник — это треугольник, в котором две стороны равны.

Углы, противоположные равным сторонам, также равны.

2) Анализ треугольников

Треугольник NOP

Основание: NO = 3 см

Боковые стороны: NP = OP = 2,1 см

Углы:

∠N = ∠O = 45° (так как треугольник равнобедренный)

∠P = 90° (прямой угол)

Треугольник DEF

Основание: DF = 1,8 см

Боковые стороны: DE = EF = 2,5 см

Углы:

∠D = ∠F = 70° (равные углы при равных сторонах)

∠E = 40° (так как сумма углов треугольника равна 180°)

Треугольник ABC

Основание: AB = 2,9 см

Боковые стороны: AC = BC = 2 см

Углы:

∠A = ∠B = 45° (равные углы при равных сторонах)

∠C = 90° (прямой угол)

3) Заключение

Все треугольники равнобедренные, и их свойства соответствуют определению равнобедренного треугольника.

Углы и стороны следует проверять, чтобы убедиться в равенстве, как указано в задаче.