
Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
ГДЗ по Математике 5 Класс Номер 501 Дорофеев, Шарыгин, Суворова — Подробные Ответы
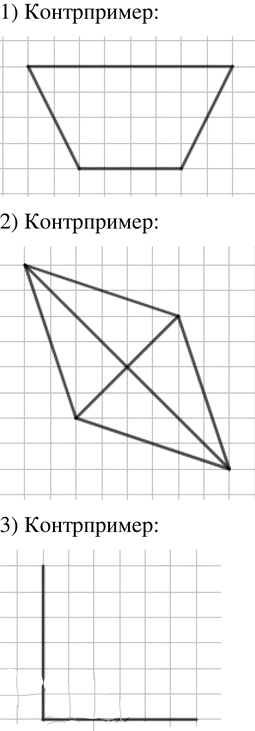
Опровергните с помощью контрпримера следующее утверждение (сделайте рисунок):
1) В любом четырёхугольнике есть прямой угол.
2) Диагонали любого четырёхугольника равны.
3) Если угол больше острого угла, то он тупой.
Прямой угол больше острого угла, но он не является тупым.
- «Диагонали любого четырёхугольника равны»: Контрпример — произвольный четырехугольник. Диагонали такого четырехугольника могут быть неравными.
- «В любом четырёхугольнике есть прямой угол»: Контрпример — ромб. Ромб является четырехугольником, но не имеет ни одного прямого угла.
- «Если угол больше острого угла, то он тупой»: Контрпример — прямоугольный треугольник. Один из углов треугольника больше острого угла (90 градусов), но при этом он не является тупым углом.
Таким образом, все три утверждения опровергаются с помощью приведенных контрпримеров.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!