Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
ГДЗ по Математике 5 Класс Номер 409 Дорофеев, Шарыгин, Суворова — Подробные Ответы
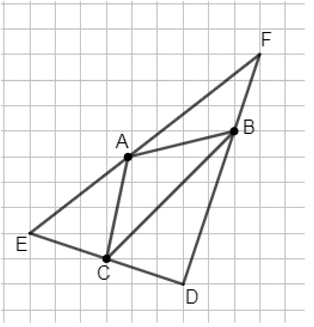
Отметьте в тетради три точки, не принадлежащие одной прямой. Начертите два треугольника так, чтобы у одного из них эти точки являлись вершинами, а у другого принадлежали его сторонам, но не являлись вершинами. Периметр какого треугольника больше?
Периметр треугольника FDE больше периметра треугольника ABC.
Ответ: периметр большего треугольника больше.
Шаг 1: Отметьте три точки
- Обозначим три точки, не принадлежащие одной прямой, как A, B и C.
Шаг 2: Постройте первый треугольник
- Используем точки A, B и C в качестве вершин треугольника ABC.
Шаг 3: Постройте второй треугольник
- Построим треугольник FDE так, чтобы точки A, B и C лежали на его сторонах, но не были его вершинами.
Шаг 4: Анализ периметров
- Треугольник FDE будет больше по размеру, чем треугольник ABC, потому что его стороны включают в себя отрезки, на которых лежат точки A, B и C, а также дополнительные сегменты, которые соединяют вершины F, D и E.
- Это означает, что периметр треугольника FDE будет больше, так как он включает в себя большее количество отрезков и, следовательно, большую общую длину.
Заключение
- Периметр треугольника FDE больше периметра треугольника ABC, так как его стороны длиннее, поскольку включают дополнительные сегменты.
Таким образом, периметр большего треугольника (FDE) больше.
