ГДЗ по Математике 5 Класс Номер 399 Дорофеев, Шарыгин, Суворова — Подробные Ответы

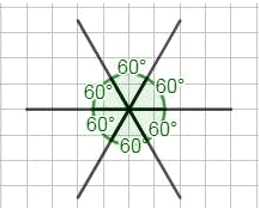
1) Сколько углов, равных 60° и имеющих общую вершину и общие с «соседями» стороны, можно построить?
Обратите внимание: углы не могут частично перекрываться.
2) Отметьте точку и проведите из неё лучи так, чтобы все углы между двумя соседними лучами были тупыми.
3) Какое наименьшее число лучей с началом в одной точке надо провести, чтобы все углы, образованные двумя соседними лучами, были острыми?

1) Можно построить шесть углов, равных 60° и имеющих общую вершину и общие с «соседями» стороны:

• три угла по 60° составляют один развернутый угол;
• еще три угла по 60° — второй развернутый угол.

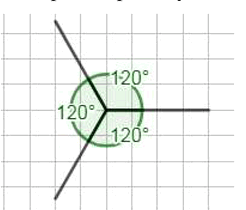
2) Можно провести три таких луча, потому что, если будет 4 луча или 2 луча, то они будут по 90° или 180°, что противоречит условию задачи (360 : 3 = 120°).

3) Из пункта 2 следует, что можно провести пять лучей (наименьшее количество), чтобы все углы, образованные двумя соседними лучами, были острыми: 360 : 5 = 72°.

Ответ: 5 лучей.

Задача

Нужно определить минимальное количество лучей, которые можно провести из одной точки, чтобы все углы между соседними лучами были острыми.

Решение

Анализ задачи:

Угол между двумя лучами, исходящими из одной точки, является острым, если он меньше 90°.

Полный круг составляет 360°.

Построение углов:

Если мы проведем только два луча, то угол между ними будет 180° (развернутый угол), что не соответствует условию.

Если провести три луча, то каждый угол будет равен 120° (360° / 3 = 120°), что также не соответствует условию, так как угол больше 90°.

Проверка с четырьмя лучами:

Если провести четыре луча, то каждый угол будет равен 90° (360° / 4 = 90°), что тоже не подходит, так как угол не острый.

Проверка с пятью лучами:

Если провести пять лучей, то каждый угол будет равен 72° (360° / 5 = 72°).

72° — это острый угол, так как он меньше 90°.

Вывод:

Минимальное количество лучей, которое необходимо провести, чтобы все углы между соседними лучами были острыми, равно пяти.

Таким образом, ответ: 5 лучей.