ГДЗ по Математике 5 Класс Номер 398 Дорофеев, Шарыгин, Суворова — Подробные Ответы

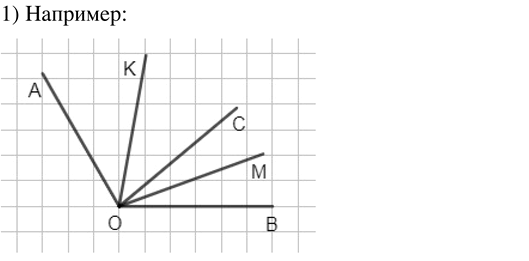
1) Следуя алгоритму, сделайте модель:
Начертите на листе бумаги угол, равный 120°; обозначьте его AOB (буквы проставьте внутри угла).
Вырежите угол
Проведите внутри угла произвольный луч OC.
Перегните ∠AO C пополам, получившуюся биссектрису обозначьте OK.
Перегните ∠BOC пополам, получившуюся биссектрису обозначьте OM.

2) Используя модель, догадайтесь, чему равна величина угла MOK.

3) Решите задачу: «Угол АОВ равен 90° (рис. 5.20). Лучи ОМ и ОK – биссектрисы углов СОВ и СОА. Найдите величину угла МОK».

2) ∠MOK = ∠AOB : 2 = 120 : 2 = 60°, потому что OK и OM биссектрисы углов AOC и COB.

3) ∠MOK = ∠AOB : 2 = 90 : 2 = 45°.

Ответ: 2) 60°; 3) 45°.

Задача 1: Угол AOB равен 120°

Построение модели:

Нарисуйте угол AOB, равный 120°.

Проведите внутри угла произвольный луч OC.

Перегните угол AOC пополам и обозначьте биссектрису как OK.

Перегните угол BOC пополам и обозначьте биссектрису как OM.

Определение угла MOK:

Поскольку OK и OM — это биссектрисы углов AOC и COB, они делят угол AOB на четыре равных части.

Угол AOB = 120°, значит каждая часть равна 30°.

Угол MOK равен сумме двух таких частей, то есть 60°.

Задача 2: Угол AOB равен 90°

Дано:

Угол AOB равен 90°.

OM и OK — биссектрисы углов COB и COA.

Решение:

Угол AOB делится на четыре равных части, так как OM и OK — биссектрисы.

Угол AOB = 90°, значит каждая часть равна 22.5°.

Угол MOK равен сумме двух таких частей, то есть 45°.

Таким образом, для угла AOB = 120° угол MOK равен 60°, а для угла AOB = 90° угол MOK равен 45°.