ГДЗ по Математике 5 Класс Номер 39 Дорофеев, Шарыгин, Суворова — Подробные Ответы

Задача

1) Отрезок АВ в 2 раза длиннее отрезка KM (рис. 1.27). Это можно записать так: АВ = 2KM. Запишите с помощью равенства: отрезок ОС в 4 раза длиннее отрезка EK; отрезок СD в 4 раза короче отрезка MK.

2) Во сколько раз отрезок AB длиннее отрезка KM, если:
а) AB = 3KM;
б) АВ = 5KM;
в) АВ = 10KM ?
Начертите пару отрезков, удовлетворяющих этому условию.
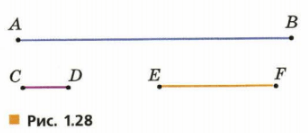
3) Измерьте отрезок AB, взяв в качестве единицы измерения отрезок CD; отрезок EF (рис. 1.28). Запишите ответ.

4) Отрезок АВ измерили отрезком CD и получили, что АВ = 10CD. Чему равна длина отрезка АВ, если CD = 3 см 5 мм?
5) Известно, что АВ = 10 см, CD = 5 мм. Запишите результат, который получится, если отрезок АВ измерить отрезком CD.

Краткий ответ:

1) OC = 4EK; MK=4CD
2) а) в три раза
б) в пять раз
в) в десять раз
3) AB =6 CD; EF = 2,5 CD
4) AB =10 CD; CD =3см 5мм
AB =10 3см 5мм =35см
5) AB =20 CD

Подробный ответ:

Запишите с помощью равенства:

ОС = 4EK

CD = MK / 4

Во сколько раз отрезок AB длиннее отрезка KM, если:
а) AB = 3KM, значит отрезок AB в 3 раза длиннее отрезка KM.
б) AB = 5KM, значит отрезок AB в 5 раз длиннее отрезка KM.
в) AB = 10KM, значит отрезок AB в 10 раз длиннее отрезка KM.

Начертите пару отрезков:

Для случая а: KM = 1 см, AB = 3 см.

Для случая б: KM = 1 см, AB = 5 см.

Для случая в: KM = 1 см, AB = 10 см.

Измерьте отрезок AB, взяв в качестве единицы измерения отрезок CD и EF (рис. 1.28):

Если длина CD = 1, то AB = 10CD.

Если длина EF = 1, то AB = 5EF.

Отрезок AB измерили отрезком CD и получили, что AB = 10CD. Чему равна длина отрезка AB, если CD = 3 см 5 мм?

CD = 3 см 5 мм = 3,5 см.

AB = 10 × 3,5 = 35 см.

Известно, что AB = 10 см, CD = 5 мм. Запишите результат, который получится, если отрезок AB измерить отрезком CD:

CD = 5 мм = 0,5 см.

AB / CD = 10 см / 0,5 см = 20.

Отрезок AB равен 20 отрезкам CD.

Оцени решение