Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
Особенности учебника:
- Понятная структура материала
Учебник логично разделен на главы, каждая из которых посвящена отдельной теме: арифметика, алгебраические выражения, геометрия и основы логики. Это позволяет учащимся постепенно углубляться в материал без перегрузки. - Практическая направленность
Авторы уделяют особое внимание применению математики в реальной жизни. Задачи часто связаны с повседневными ситуациями, что делает обучение более увлекательным и полезным. - Интерактивные задания
В книге встречаются задачи на построение, головоломки и упражнения, требующие нестандартного подхода. Это стимулирует творческое мышление и помогает ученикам не просто запоминать формулы, а понимать их суть. - Материал для разного уровня подготовки
Учебник подходит как для сильных учеников, так и для тех, кто только начинает осваивать основы математики. Задания варьируются от простых до более сложных, что позволяет каждому ученику работать в своем темпе. - Красочное оформление
Иллюстрации, таблицы и схемы делают материал более доступным и визуально привлекательным для школьников.
Почему стоит выбрать этот учебник?
Дорофеев и Шарыгин создали пособие, которое не только соответствует образовательным стандартам, но и вдохновляет учеников на изучение математики. Учебник учит не просто решать задачи, а мыслить аналитически, искать закономерности и применять знания в жизни. Его использование в образовательном процессе помогает школьникам сформировать прочную базу для дальнейшего изучения математики.
ГДЗ по Математике 5 Класс Номер 381 Дорофеев, Шарыгин, Суворова — Подробные Ответы
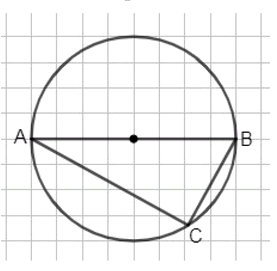
1) Постройте окружность и проведите её диаметр АВ. Постройте угол АСВ с вершиной С, лежащей на окружности. Каким (острым, прямым или тупым) является этот угол?
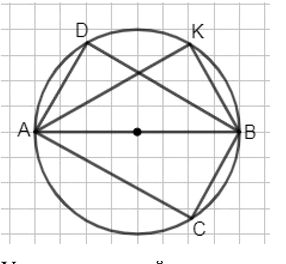
2) Постройте ещё два угла с вершинами на окружности, опирающиеся на диаметр, и ответьте на тот же вопрос. Сопоставьте свои наблюдения с наблюдениями одноклассников. Закончите вывод: «Угол с вершиной на окружности, опирающийся на её диаметр, является…»
3) Как построить прямой угол, имея только циркуль и линейку?
1) ∠ACB — прямой:
2) ∠ADB и ∠AKB — прямые:
Угол с вершиной на окружности, опирающийся на её диаметр, является прямым.
3) Чтобы построить прямой угол, имея только циркуль и линейку, нужно:
- начертить окружность;
- провести её диаметр;
- отметить точку, лежащую на окружности;
- построить угол с вершиной на окружности и опирающийся на диаметр.
1) Угол АСВ
Когда точка C лежит на окружности, и угол АСВ опирается на диаметр АВ, этот угол всегда будет прямым. Это связано с теоремой о вписанном угле, которая утверждает, что угол, опирающийся на диаметр окружности, равен 90 градусам.
2) Постройка дополнительных углов
Построив еще два угла с вершинами на окружности, которые также опираются на диаметр, вы заметите, что оба они также будут прямыми. Это наблюдение будет совпадать с наблюдениями ваших одноклассников.
Таким образом, можно сделать вывод: «Угол с вершиной на окружности, опирающийся на её диаметр, является прямым».
3) Постройка прямого угла с помощью циркуля и линейки
Чтобы построить прямой угол, имея только циркуль и линейку, выполните следующие шаги:
- Постройте окружность: Используйте циркуль, чтобы нарисовать окружность произвольного радиуса.
- Проведите диаметр: С помощью линейки проведите прямую линию через центр окружности, которая будет диаметром.
- Постройте угол: Выберите любую точку на окружности, отличную от концов диаметра, и соедините её с концами диаметра. Угол, образованный этими двумя линиями, будет прямым.
Этот метод использует свойства окружности и диаметра для построения прямого угла.
Математика
