ГДЗ по Математике 5 Класс Номер 379 Дорофеев, Шарыгин, Суворова — Подробные Ответы

1) Начертите какой-нибудь острый угол и постройте угол, дополняющий его до развёрнутого угла. Начертите тупой угол. Постройте угол, дополняющий его до развёрнутого угла.
2) Пусть углы АОВ и ВОС составляют развёрнутый угол. Каким является угол ВОС, если угол АОВ: а) острый; б) прямой; в) тупой?

1) Построение углов

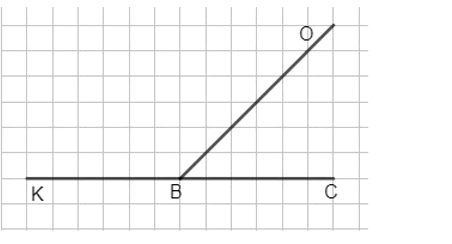
• Острый угол: Например, 40°. Дополняющий до развёрнутого: 140°.
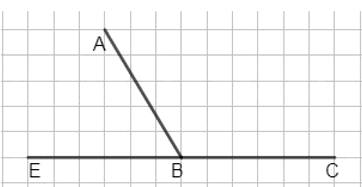
• Тупой угол: Например, 120°. Дополняющий до развёрнутого: 60°.

2) Угол ВОС при разных углах АОВ

• АОВ острый: ВОС = 140° (тупой).
• АОВ прямой: ВОС = 90° (прямой).
• АОВ тупой: ВОС = 60° (острый).

1) Построение углов

Острый угол и дополнение до развёрнутого угла

• Начертите острый угол:
• Например, угол 40°.
• Постройте угол, дополняющий его до развёрнутого угла:
• Развёрнутый угол равен 180°.
• Дополняющий угол: 180° — 40° = 140°.

Тупой угол и дополнение до развёрнутого угла

Начертите тупой угол:

• Например, угол 120°.

Постройте угол, дополняющий его до развёрнутого угла:

• Дополняющий угол: 180° — 120° = 60°.

2) Угол ВОС при различных углах АОВ

Если углы АОВ и ВОС составляют развёрнутый угол (180°), то:

• а) Угол АОВ острый (например, 40°):
  • Угол ВОС = 180° — 40° = 140° (тупой).
• б) Угол АОВ прямой (90°):
  • Угол ВОС = 180° — 90° = 90° (прямой).
• в) Угол АОВ тупой (например, 120°):
  • Угол ВОС = 180° — 120° = 60° (острый).