
Учебник «Математика. 5 класс», написанный выдающимися авторами А. Г. Дорофеевым и И. Ф. Шарыгиным, является одним из наиболее популярных и эффективных пособий для школьников. Этот учебник помогает не только освоить базовые математические навыки, но и развить логическое мышление, внимание и интерес к предмету. Благодаря своей структуре, ярким примерам и увлекательным задачам, он легко становится надежным помощником в изучении математики.
ГДЗ по Математике 5 Класс Номер 108 Дорофеев, Шарыгин, Суворова — Подробные Ответы
На координатной прямой точками отмечены натуральные числа а, b, с и d (рис. 2.9). Какие из неравенств являются верными?
1) а > с. 2) b > с. 3) d < а.
4) а < b. 5) d < а < с. 6) b < с < а.
- а > с — неверно
- b > с — верно
- d < а — верно
- а < b — верно
- d < а < с — верно
- b < с < а — неверно
1) Внимательно изучаем координатную прямую, на которой отмечены точки a, b, c и d.
2) Сравниваем положение этих точек на прямой:
- Точка d находится левее точки a
- Точка a находится левее точки c
- Точка b находится правее точки a
3) Исходя из этого, можно сделать следующие выводы:
- a > c — неверно, так как a находится левее c
- b > c — верно, так как b находится правее c
- d < a — верно, так как d находится левее a
- a < b — верно, так как a находится левее b
- d < a < c — верно, так как d находится левее a, а a находится левее c
- b < c < a — неверно, так как b находится левее c, а c находится левее a
4) Таким образом, мы последовательно проверяем каждое из неравенств, сравнивая расположение точек на координатной прямой.
5) Фиксируем верные и неверные неравенства, делая окончательный вывод.
Ключевым моментом в решении является внимательное изучение расположения точек на координатной прямой и последовательное сравнение их положений. Это позволяет определить, какие из предложенных неравенств являются верными, а какие — нет.



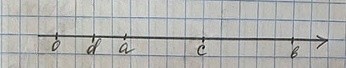


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!