Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 9 Класс Номер 24 Дорофеев, Суворова — Подробные Ответы
Если при выполнении какой-нибудь арифметической операции с любыми двумя числами из
некоторого множества получается число из этого же множества, то говорят, что данное
множество чисел замкнуто относительно этой операции. Например, множество натуральных
чисел N замкнуто относительно сложения и не замкнуто относительно вычитания.
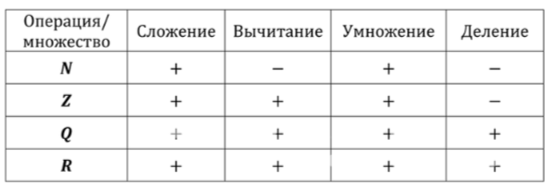
Заполните таблицу, используя знак «+», если множество замкнуто относительно указанной
операции, и знак «-», если оно не замкнуто:
Почему говорят, что арифметика целых чисел «богаче», чем арифметика натуральных чисел?
арифметика рациональных чисел «богаче», чем арифметика целых чисел?
1)Множество целых чисел замкнуто относительно трех арифметических операций, а множество натуральных чисел — относительно двух операций, поэтому говорят, что арифметика целых чисел богаче, чем арифметика натуральных чисел;
2)Множество рациональных чисел замкнуто относительно четырех арифметических операций, а множество целых чисел — относительно трех операций, поэтому говорят, что арифметика рациональных чисел богаче, чем арифметика целых чисел.
1)Рассмотрим множество натуральных чисел . Натуральные числа включают все положительные целые числа, то есть . Натуральные числа замкнуты относительно сложения и умножения, что означает, что результат сложения и умножения любых двух натуральных чисел также является натуральным числом. Однако, множество натуральных чисел не замкнуто относительно вычитания и деления, поскольку результат вычитания или деления двух натуральных чисел может не быть натуральным числом. Например, , что не является натуральным числом. Таким образом, арифметика натуральных чисел ограничена только операциями сложения и умножения.
Теперь рассмотрим множество целых чисел , которое включает как положительные, так и отрицательные целые числа, а также ноль, то есть . Множество целых чисел замкнуто относительно сложения, вычитания и умножения, что означает, что результат этих операций с целыми числами всегда остается целым числом. Например, , , . Однако, множество целых чисел не замкнуто относительно деления, так как результат деления двух целых чисел может быть нецелым. Например, , что не является целым числом. Поэтому говорят, что арифметика целых чисел богаче, чем арифметика натуральных чисел, так как она позволяет больше операций: вычитание и умножение наряду с сложением, в отличие от натуральных чисел.
2)Теперь рассмотрим множество рациональных чисел . Рациональные числа включают все числа, которые могут быть записаны в виде дроби , где и — целые числа, и . Например, . Множество рациональных чисел замкнуто относительно всех четырех арифметических операций: сложения, вычитания, умножения и деления. Это означает, что результат этих операций с рациональными числами всегда остается рациональным числом. Например, , , , . Таким образом, арифметика рациональных чисел богаче, чем арифметика целых чисел, так как рациональные числа позволяют выполнять все четыре арифметические операции.
Поскольку множество рациональных чисел замкнуто относительно всех четырех операций, а множество целых чисел — только относительно трех, говорят, что арифметика рациональных чисел богаче, чем арифметика целых чисел.
Алгебра