Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 9 Класс Номер 233 Дорофеев, Суворова — Подробные Ответы
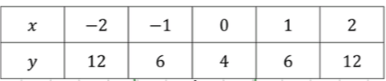
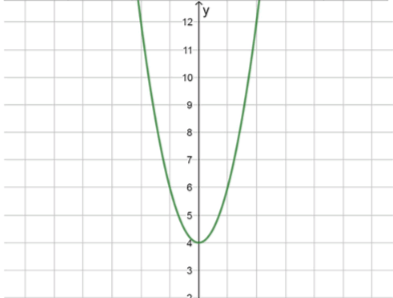
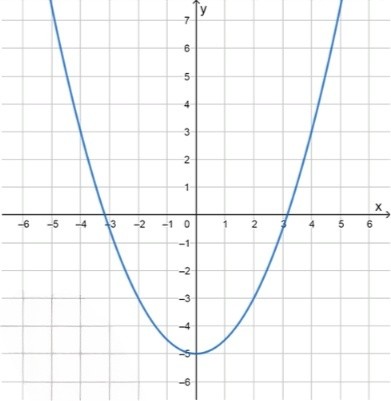
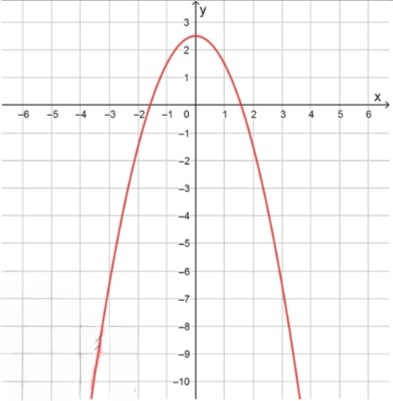
Изобразите схематически график функции и задайте эту функцию формулой, если известно, что её график получен сдвигом вдоль оси у:
а) параболы на 4 единицы вверх;
б) параболы на 5 единиц вниз;
в) параболы на 2,5 единицы вверх;
г) параболы на 1,5 единицы вниз.
а)
В данной задаче рассматривается парабола, которая имеет стандартное уравнение вида , где — это коэффициент, который определяет форму параболы, а — это вертикальный сдвиг. Исходная парабола имеет вид , что является стандартной параболой с открывающейся вверх ветвью, где коэффициент при равен . Увеличение коэффициента (в данном случае до 2) делает параболу более узкой, то есть ветви параболы становятся более крутыми.
Теперь мы добавляем к правой части уравнения, что означает сдвиг параболы вверх на 4 единицы. Это сдвигает все точки параболы, включая её вершину, на 4 единицы выше, но форма самой параболы не изменится.
Таким образом, уравнение после сдвига будет:
где вершина параболы , так как она была сдвинута вверх от исходной вершины .
б)
Здесь у нас исходная парабола , где коэффициент при говорит о том, что ветви параболы будут более широкими по сравнению с параболой , так как коэффициент меньше 1.
В данном уравнении добавлен сдвиг на . Это означает, что парабола будет сдвинута вниз на 5 единиц. Парабола, исходно расположенная на оси с вершиной в точке , после сдвига вниз будет иметь вершину в точке .
Итак, уравнение после сдвига:
где вершина параболы теперь будет в точке .
в)
В этом случае у нас исходная парабола , где коэффициент при делает параболу, открывающуюся вниз. Эта парабола имеет вершину в точке , и её ветви направлены вниз.
Добавление к правой части уравнения означает, что парабола будет сдвинута вверх на 2,5 единицы. Таким образом, вершина параболы, которая была в , сдвигается в точку , но форма параболы остаётся такой же, с открывающимися вниз ветвями.
Конечное уравнение:
где вершина теперь будет находиться в точке .
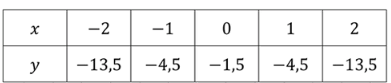
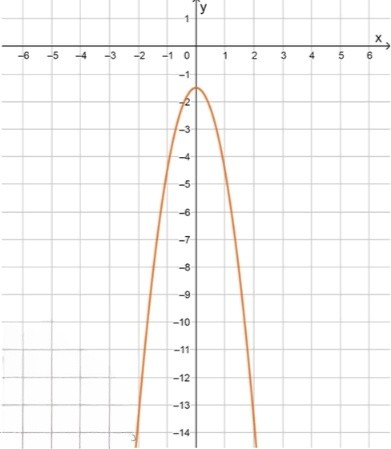
г)
Исходная парабола имеет коэффициент , что означает, что она открывается вниз и более крута по сравнению с параболой , так как коэффициент больше по абсолютной величине, чем . Ветви параболы будут направлены вниз и будут более сжатыми.
Теперь добавляем , что представляет собой сдвиг параболы вниз на 1,5 единицы. Таким образом, вершина параболы, которая была в точке , после сдвига будет находиться в точке , а форма параболы останется прежней.
Конечное уравнение:
где вершина параболы теперь находится в точке .
Алгебра