Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 9 Класс Номер 229 Дорофеев, Суворова — Подробные Ответы
Постройте график функции:
— уравнение прямой:
— уравнение параболы:
Точка с абсциссой равной 1 принадлежит графику функции ; для графика функции — эта точка указана как проколотая (то есть не включена в область определения).
Ответ: График построен.
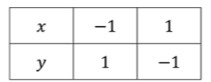
— уравнение прямой:
Функция представляет собой прямую линию с угловым коэффициентом . Эта прямая будет иметь отрицательный наклон и будет пересекать ось в точке . График прямой, описывающей уравнение , будет двигаться влево и вправо, образуя угол 45° с осями.
Для вычисления значений при различных , подставим следующие значения :
- При , .
- При , .
Это подтверждается таблицей значений:
Значения для при этих подтвердили, что прямая проходит через точки и .
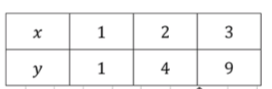
— уравнение параболы:
Функция представляет собой стандартную параболу, открывающуюся вверх. Вершина параболы находится в точке , и она симметрична относительно оси . Чем дальше от оси , тем больше увеличиваются значения . Парабола будет двигаться вверх по мере увеличения .
Для вычисления значений при различных , подставим следующие значения :
- При , .
- При , .
- При , .
Это подтверждается таблицей значений:
Значения для при этих подтверждают, что парабола проходит через точки , и .
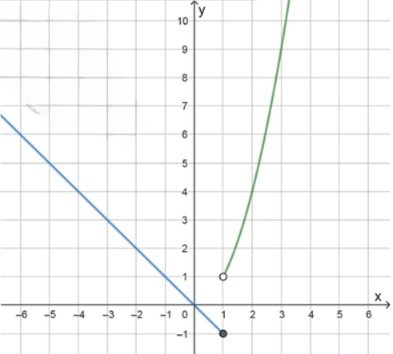
График функции:
График состоит из двух частей:
- Для , график будет прямой , который имеет угловой коэффициент и проходит через точку , направленной вниз и влево.
- Для , график будет параболой , начинающейся в точке , направленной вверх, где значения будут возрастать по мере увеличения .
Для точка будет принадлежать и прямой, и параболе, но при построении графика парабола не будет включать точку , так как для в уравнении параболы не присутствует эта точка. Точка будет обозначена как проколотая, так как она не включена в область определения для параболы.
Ответ: График построен.
Алгебра