ГДЗ по Алгебре 9 Класс Номер 221 Дорофеев, Суворова — Подробные Ответы

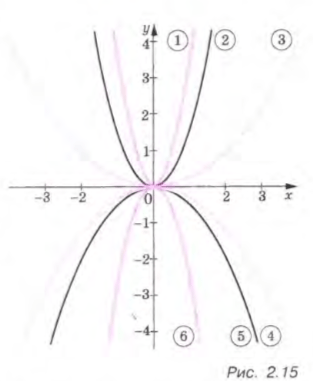
На рисунке 2.15 даны графики квадратичных функций, заданных формулами:

$$y = 3.2x^2, \quad y = -0.6x^2, \quad y = 1.6x^2, \quad y = -\frac{1}{2}x^2, \quad y = -\frac{1}{3}x^2, \quad y = \frac{1}{4}x^2.$$

Соотнесите каждый из них с одной из формул.

У функции вида $y = ax^2$:

Если $a > 0$, то ветви параболы направлены вверх;

Если $a < 0$, то ветви параболы направлены вниз;

Чем больше по модулю параметр $a$, тем больше «крутизна» графика.

$y = 3.2x^2$;

$y = 1.6x^2$;

$y = \frac{1}{4}x^2$;

$y = -\frac{1}{3}x^2$;

$y = -0.6x^2$;

$y = -2\frac{1}{2}x^2$.

У функции вида $y = ax^2$:

Если $a > 0$, то ветви параболы направлены вверх. Это означает, что для любого положительного значения $a$ парабола будет открываться вверх. Это также значит, что вершина параболы будет представлять собой точку минимума функции, а значения функции будут увеличиваться по мере удаления от оси симметрии (оси $y$).

Если $a < 0$, то ветви параболы направлены вниз. В этом случае парабола будет открываться вниз, а её вершина будет точкой максимума. Значения функции будут уменьшаться по мере удаления от оси симметрии.

Чем больше по модулю параметр $a$, тем больше «крутизна» графика. Если $a$ больше по модулю, то парабола будет более крутой, и её ветви будут располагаться ближе друг к другу. Если $a$ меньше по модулю, то парабола будет более «плоской», и её ветви будут более широко расставлены.

$y = 3.2x^2$:
Параметр $a = 3.2$ положителен, значит парабола открывается вверх. Поскольку $|a| = 3.2$ — значение относительно большое, то парабола будет достаточно крутой, и её ветви будут расположены близко друг к другу. Это означает, что функция будет быстро увеличиваться по мере удаления от вершины.

$y = 1.6x^2$:
Параметр $a = 1.6$ положителен, значит парабола также открывается вверх. Значение $|a| = 1.6$ меньше, чем в предыдущем случае, что означает, что парабола будет менее крутой по сравнению с $y = 3.2x^2$. Ветви будут немного шире, и функция будет увеличиваться более постепенно.

$y = \frac{1}{4}x^2$:
Параметр $a = \frac{1}{4}$ положителен, значит парабола открывается вверх. Здесь $|a| = \frac{1}{4}$, что является очень маленьким значением. Это означает, что парабола будет очень «плоской», с широко расставленными ветвями, и функция будет увеличиваться медленно.

$y = -\frac{1}{3}x^2$:
Параметр $a = -\frac{1}{3}$ отрицателен, значит парабола открывается вниз. Значение $|a| = \frac{1}{3}$ невелико, что означает, что парабола будет не слишком крутой. Она будет иметь умеренную крутизну и будет убывать на участке, удаляющемся от вершины.

$y = -0.6x^2$:
Параметр $a = -0.6$ отрицателен, значит парабола открывается вниз. Значение $|a| = 0.6$ также не слишком велико, поэтому парабола будет немного шире, чем у функции $y = -2.5x^2$. Ветви будут относительно широко расставлены, и функция будет убывать не так резко, как у более крупных значений $a$.

$y = -2.5x^2$:
Параметр $a = -2.5$ отрицателен, значит парабола открывается вниз. Поскольку $|a| = 2.5$, это довольно большое значение, и парабола будет достаточно крутой. Ветви будут направлены вниз и расположены относительно близко друг к другу, что означает, что функция будет быстро убывать по мере удаления от вершины.