ГДЗ по Алгебре 9 Класс Номер 210 Дорофеев, Суворова — Подробные Ответы

Постройте график функции, воспользовавшись алгоритмом, предложенным в предыдущем упражнении:
a) $y=2x^2-2x-12$;
б) $y=-2x^2+6x$.

а) Функция: $y=2x^2-2x-12$

1)Точки пересечения параболы с осью $x$ (нули функции): $2x^2-2x-12=0\mathrm{\mid }:2;x^2-x-6=0;D=1+4\cdot 6=1+24=25,\text{ тогда}:$
$x_1=\frac{1-5}{2}=-2\text{ и }{x}_2=\frac{1+5}{2}=3;$

2)Ось симметрии равноудалена от точек с равными ординатами:
$x=\frac{3-2}{2}=\frac{1}{2};$

3)Координаты вершины параболы:
$x=\frac{1}{2}\text{ и }y\left(\frac{1}{2}\right)=2\cdot 0,5^2-2\cdot 0,5-12=2\cdot 0,25-1-12=-12,5;$

4)Координаты некоторых других точек:
$y(-1)=2\cdot (-1{)}^2-2\cdot (-1)-12=2+2-12=-8;$
$y(0)=2\cdot 0^2-2\cdot 0-12=0-12=-12;$
$y(1)=2\cdot 1^2-2\cdot 1-12=2-2-12=-12;$
$y(2)=2\cdot 2^2-2\cdot 2-12=2\cdot 4-4-12=-8;$

5)График функции:

б) Функция: $y=-2x^2+6x$

1)Точки пересечения параболы с осью $x$ (нули функции): $-2x^2+6x=0\mathrm{\mid }:(-2);x^2-3x=0;x(x-3)=0,\text{ тогда}:$
$x_1=0,x_2=3;$

2)Ось симметрии равноудалена от точек с равными ординатами:
$x=\frac{3+0}{2}=1,5;$

3)Координаты вершины параболы:
$x=1,5\text{ и }y(1,5)=-2\cdot 1,5^2+6\cdot 1,5=-2\cdot 2,25+9=-4,5+9=4,5;$

4)Координаты некоторых других точек:
$y(-1)=-2\cdot (-1{)}^2+6\cdot (-1)=-2-6=-8;$
$y(1)=-2\cdot 1^2+6\cdot 1=-2+6=4;$
$y(2)=-2\cdot 2^2+6\cdot 2=-2\cdot 4+12=-8+12=4;$
$y(4)=-2\cdot 4^2+6\cdot 4=-2\cdot 16+24=-32+24=-8;$

5)График функции:

а) Функция: $y=2x^2-2x-12$

1)Точки пересечения параболы с осью $x$ (нули функции):

Чтобы найти точки пересечения параболы с осью $x$, необходимо решить уравнение $2x^2-2x-12=0$. Для этого первым шагом поделим обе стороны уравнения на 2:

$$\frac{2x^2-2x-12}{2}=0\Rightarrow x^2-x-6=0.$$

Теперь решим это уравнение с помощью дискриминанта. Напоминаем, что для квадратичного уравнения $a{x}^2+bx+c=0$ дискриминант $D$ вычисляется по формуле:

$$D=b^2-4ac\mathrm{.}$$

В данном случае $a=1$, $b=-1$, $c=-6$, подставим эти значения в формулу для дискриминанта:

$$D=(-1{)}^2-4\cdot 1\cdot (-6)=1+24=25.$$

Дискриминант положительный, следовательно, у уравнения есть два корня. Найдем их с помощью формулы:

$$x_1=\frac{-b-\sqrt{D}}{2a}=\frac{-(-1)-\sqrt{25}}{2\cdot 1}=\frac{1-5}{2}=-2,$$

$$$$$$x_2=\frac{-b+\sqrt{D}}{2a}=\frac{-(-1)+\sqrt{25}}{2\cdot 1}=\frac{1+5}{2}=3.$$

Таким образом, точки пересечения параболы с осью $x$ — это $x_1=-2$ и $x_2=3$.

2)Ось симметрии параболы:

Ось симметрии параболы проходит через точку, которая является серединой отрезка, соединяющего точки пересечения параболы с осью $x$. Эта точка находится по формуле:

$$x=\frac{x_1+x_2}{2}=\frac{-2+3}{2}=\frac{1}{2}\mathrm{.}$$

Таким образом, ось симметрии параболы — это прямая $x=\frac{1}{2}$.

3)Координаты вершины параболы:

Вершина параболы находится на оси симметрии. Чтобы найти ординату вершины, подставим значение $x=\frac{1}{2}$ в уравнение функции:

$$y\left(\frac{1}{2}\right)=2\cdot {\left(\frac{1}{2}\right)}^2-2\cdot \left(\frac{1}{2}\right)-12=2\cdot 0.25-1-12=0.5-1-12=-\mathrm{12.5.}$$

Таким образом, координаты вершины параболы — $(\frac{1}{2},-12.5)$.

4)Координаты некоторых других точек:

Для более точного построения графика, найдем координаты нескольких дополнительных точек.

• $y(-1)$:

$$y(-1)=2\cdot (-1{)}^2-2\cdot (-1)-12=2\cdot 1+2-12=2+2-12=-8.$$

• $y(0)$:

$$y(0)=2\cdot 0^2-2\cdot 0-12=0-0-12=-12.$$

• $y(1)$:

$$y(1)=2\cdot 1^2-2\cdot 1-12=2-2-12=-12.$$

• $y(2)$:

$$y(2)=2\cdot 2^2-2\cdot 2-12=2\cdot 4-4-12=8-4-12=-8.$$

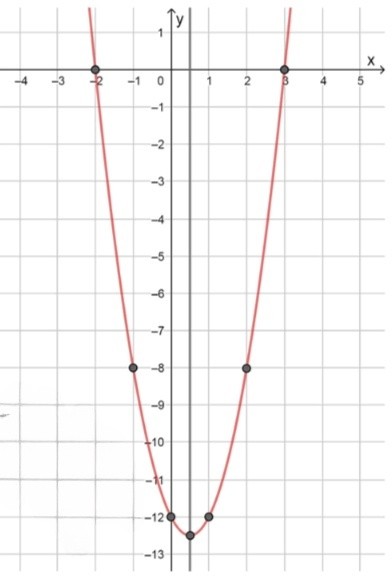
5)График функции:

Теперь, зная все необходимые точки, можно построить график функции. На нем будут отмечены следующие точки: $(-1,-8)$, $(0,-12)$, $(1,-12)$, $(2,-8)$, а также вершина $(\frac{1}{2},-12.5)$. Эти точки следует соединить плавной линией, образующей график параболы, которая открывается вверх и имеет ось симметрии $x=\frac{1}{2}$.

б) Функция: $y=-2x^2+6x$

1)Точки пересечения параболы с осью $x$ (нули функции):

Для нахождения точек пересечения параболы с осью $x$, решим уравнение $-2x^2+6x=0$. Вынесем общий множитель $-2x$:

$$-2x(x-3)=0.$$

Из этого уравнения получаем два корня:

$$x_1=0,x_2=3.$$

Таким образом, точки пересечения параболы с осью $x$ — это $x_1=0$ и $x_2=3$.

2)Ось симметрии параболы:

Ось симметрии параболы проходит через точку, которая является серединой отрезка, соединяющего точки пересечения параболы с осью $x$. Эта точка находится по формуле:

$$x=\frac{x_1+x_2}{2}=\frac{0+3}{2}=\mathrm{1.5.}$$

Таким образом, ось симметрии параболы — это прямая $x=1.5$.

3)Координаты вершины параболы:

Вершина параболы находится на оси симметрии. Чтобы найти ординату вершины, подставим значение $x=1.5$ в уравнение функции:

$$y(1.5)=-2\cdot (1.5{)}^2+6\cdot (1.5)=-2\cdot 2.25+9=-4.5+9=\mathrm{4.5.}$$

Таким образом, координаты вершины параболы — $(1.5,4.5)$.

4)Координаты некоторых других точек:

Для более точного построения графика, найдем координаты нескольких дополнительных точек.

• $y(-1)$:

$$y(-1)=-2\cdot (-1{)}^2+6\cdot (-1)=-2-6=-8.$$

• $y(1)$:

$$y(1)=-2\cdot 1^2+6\cdot 1=-2+6=4.$$

• $y(2)$:

$$y(2)=-2\cdot 2^2+6\cdot 2=-2\cdot 4+12=-8+12=4.$$

• $y(4)$:

$$y(4)=-2\cdot 4^2+6\cdot 4=-2\cdot 16+24=-32+24=-8.$$

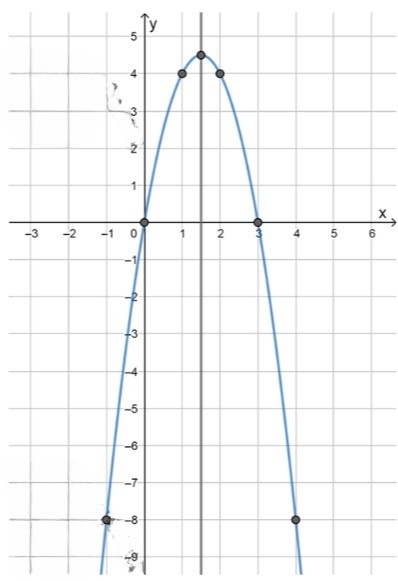
5)График функции:

Теперь, зная все необходимые точки, можно построить график функции. На нем будут отмечены следующие точки: $(-1,-8)$, $(1,4)$, $(2,4)$, $(4,-8)$, а также вершина $(1.5,4.5)$. Эти точки следует соединить плавной линией, образующей график параболы, которая открывается вниз и имеет ось симметрии $x=1.5$.