ГДЗ по Алгебре 9 Класс Номер 201 Дорофеев, Суворова — Подробные Ответы

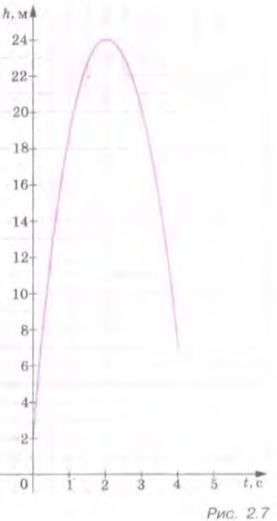
С двухметровой высоты под углом к горизонту выпущена сигнальная ракета. Изменение высоты ее полета $h$ (в метрах) в зависимости от времени движения $t$ (в секундах) описывается формулой

$$h = 2 + 21t — 5t^2.$$

График функции $h = f(t)$ изображен на рисунке 2.7. Используя график, ответьте на вопросы:

1)В какое время ракета поднимется на высоту 20 м и в какое время она окажется на той же высоте при спуске?

2)На какой высоте ракета будет через 3,5 с полета? Через сколько секунд после начала полета ракета уже была на той же высоте?

3)Укажите наибольшую высоту подъема ракеты. Сколько времени потребовалось ракете, чтобы подняться на максимальную высоту?

4)Как вы думаете, почему график не доведен до пересечения с осью $x$?

1)Ракета будет на высоте 20 метров:

При подъеме через $\approx 1,1$ с;

При спуске через 3 с после запуска;

2)Через 3,5 с полета ракета будет на высоте 15 м;
На этой же высоте она была через $\approx 0,75$ с после начала полета;

3)Максимальная высота подъема ракеты равна 24 м;
Ракета будет на этой высоте через 2 с после начала полета;

4)График не доведен до пересечения с осью $x$, так как место, в котором упала ракета, находится выше места, с которого ее запустили.

1)Ракета будет на высоте 20 метров:

Для нахождения времени, когда ракета будет на высоте 20 метров, нужно решить уравнение для $h = 20$:

$$20 = 2 + 21t — 5t^2$$

Переносим все элементы на одну сторону:

$$0 = -5t^2 + 21t — 18$$

Теперь решаем это квадратное уравнение с помощью формулы:

$$t = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a}$$

где $a = -5$, $b = 21$, $c = -18$. Подставляем значения:

$$t = \frac{-21 \pm \sqrt{21^2 — 4(-5)(-18)}}{2(-5)} = \frac{-21 \pm \sqrt{441 — 360}}{-10} = \frac{-21 \pm \sqrt{81}}{-10} = \frac{-21 \pm 9}{-10}$$

Таким образом, два корня:

$$t = \frac{-21 + 9}{-10} = \frac{-12}{-10} = 1,2 \quad \text{или} \quad t = \frac{-21 — 9}{-10} = \frac{-30}{-10} = 3$$

Таким образом, ракета поднимется на высоту 20 метров через $\approx 1,1$ с при подъеме и через 3 с при спуске.

2)Через 3,5 с полета ракета будет на высоте 15 м:

Для нахождения высоты ракеты через 3,5 с, подставим $t = 3,5$ в уравнение:

$$h = 2 + 21(3,5) — 5(3,5)^2 = 2 + 73,5 — 5(12,25) = 2 + 73,5 — 61,25 = 14,25$$

Таким образом, ракета будет на высоте 15 м через $t = 3,5$ с полета.

Теперь находим, когда ракета будет на той же высоте, что и при $t = 0,75$. Для этого решим уравнение $h = 15$:

$$15 = 2 + 21t — 5t^2$$

Переносим все элементы на одну сторону:

$$0 = -5t^2 + 21t — 13$$

Решаем это квадратное уравнение:

$$t = \frac{-21 \pm \sqrt{21^2 — 4(-5)(-13)}}{2(-5)} = \frac{-21 \pm \sqrt{441 — 260}}{-10} = \frac{-21 \pm \sqrt{181}}{-10}$$

Получаем два корня:

$$t \approx 0,75 \quad \text{или} \quad t \approx 3,25$$

На той же высоте ракета была через $\approx 0,75$ с.

3)Максимальная высота подъема ракеты:

Максимальная высота ракеты достигается в вершине параболы. Абсцисса вершины параболы находится по формуле:

$$t = \frac{-b}{2a}$$

где $a = -5$, $b = 21$. Подставляем значения:

$$t = \frac{-21}{2(-5)} = \frac{-21}{-10} = 2,1$$

Теперь подставляем это значение в исходное уравнение для нахождения максимальной высоты:

$$h = 2 + 21(2,1) — 5(2,1)^2 = 2 + 44,1 — 5(4,41) = 2 + 44,1 — 22,05 = 24,05$$

Таким образом, максимальная высота ракеты составляет $24$ м, и она достигается через 2 с после начала полета.

4)Почему график не доведен до пересечения с осью $x$:

График не доведен до пересечения с осью $x$, потому что ракета не упала на землю в момент, когда её высота стала бы равной нулю. Место, где ракета упала, находится выше уровня старта, то есть ракета в конечном итоге не достигла земли, и её траектория не пересекла ось $x$.