ГДЗ по Алгебре 9 Класс Номер 199 Дорофеев, Суворова — Подробные Ответы

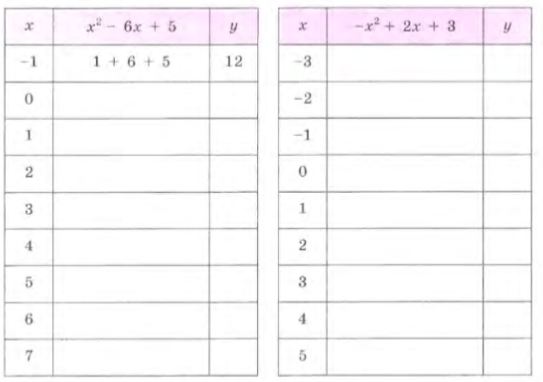
Заполните таблицу значений функции и постройте ее график:

а) $y = x^2 — 6x + 5;$
б) $y=-x^2+2x+3;$$$

$y = -x^2 + 2x + 3;$В каждом случае ответьте на вопросы:

1)Имеет ли функция наименьшее или наибольшее значение, и чему оно равно? При каком $x$ функция принимает это значение?

2)Пересекает ли график функции прямую $y = 10$? $y = -10$?

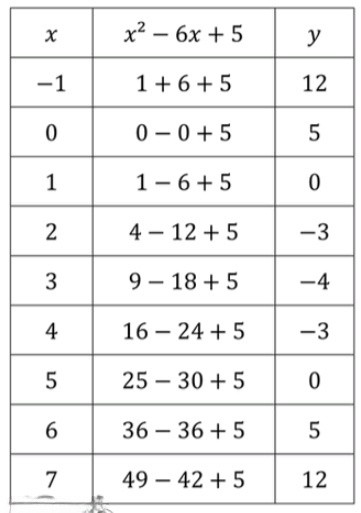
а) $y=x^2-6x+5;$

$y = x^2 — 6x + 5;$

1)Имеет наименьшее значение: $y_{\text{min}} = -4$ при $x = 3;$

2)Пересекает прямую: $y = 10;$

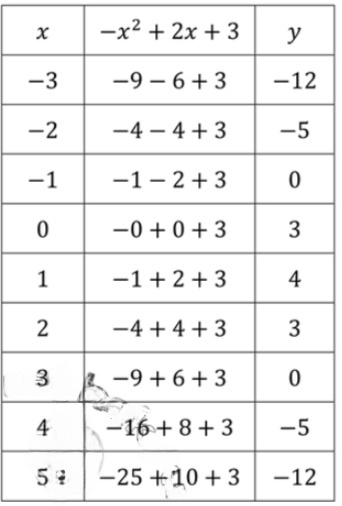
б) $y=-x^2+2x+3;$

$y = -x^2 + 2x + 3;$

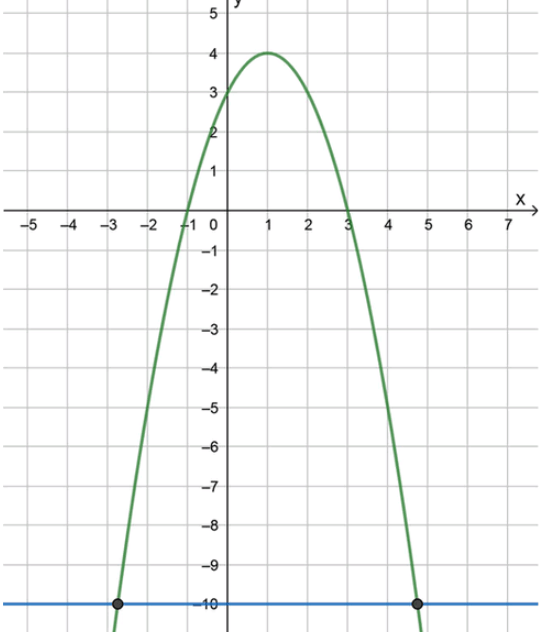
1)Имеет наибольшее значение: $y_{\text{max}} = 4$ при $x = 1;$

2)Пересекает прямую: $y = -10;$

а) $y = x^2 — 6x + 5;$

1)Для нахождения наименьшего значения функции $y = x^2 — 6x + 5$ необходимо привести её к каноническому виду. Для этого найдём вершину параболы, используя формулу для абсциссы вершины:

$$x = \frac{-b}{2a}$$

где $a = 1$, $b = -6$. Подставляем значения:

$$x = \frac{-(-6)}{2(1)} = \frac{6}{2} = 3$$

Теперь подставим найденное значение $x = 3$ в исходную функцию для нахождения соответствующего значения $y$:

$$y = (3)^2 — 6(3) + 5 = 9 — 18 + 5 = -4$$

Таким образом, наименьшее значение функции равно $y_{\text{min}} = -4$, и оно достигается при $x = 3$.

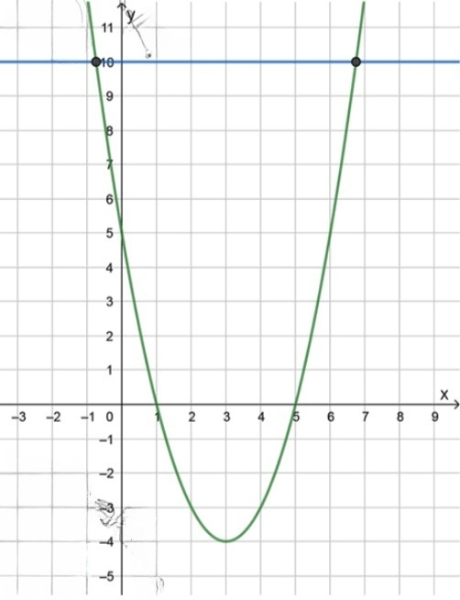
2)Для того чтобы узнать, пересекает ли график функции прямую $y = 10$, нужно решить уравнение:

$$x^2 — 6x + 5 = 10$$

Переносим 10 влево:

$$x^2 — 6x — 5 = 0$$

Решаем квадратное уравнение по формуле:

$$x = \frac{-(-6) \pm \sqrt{(-6)^2 — 4(1)(-5)}}{2(1)} = \frac{6 \pm \sqrt{36 + 20}}{2} = \frac{6 \pm \sqrt{56}}{2} = \frac{6 \pm 2\sqrt{14}}{2}$$

Получаем два корня:

$$x = 3 + \sqrt{14} \quad \text{или} \quad x = 3 — \sqrt{14}$$

Таким образом, график функции пересекает прямую $y = 10$ в двух точках.

б) $y = -x^2 + 2x + 3;$

1)Для нахождения наибольшего значения функции $y = -x^2 + 2x + 3$, также используем формулу для абсциссы вершины параболы. Здесь $a = -1$, $b = 2$. Подставляем значения:

$$x = \frac{-2}{2(-1)} = \frac{-2}{-2} = 1$$

Теперь подставим найденное значение $x = 1$ в исходную функцию:

$$y = -(1)^2 + 2(1) + 3 = -1 + 2 + 3 = 4$$

Таким образом, наибольшее значение функции равно $y_{\text{max}} = 4$, и оно достигается при $x = 1$.

2)Чтобы узнать, пересекает ли график функции прямую $y = -10$, решим уравнение:

$$-x^2 + 2x + 3 = -10$$

Переносим $-10$ влево:

$$-x^2 + 2x + 13 = 0$$

Умножаем обе части уравнения на -1:

$$x^2 — 2x — 13 = 0$$

Решаем квадратное уравнение по формуле:

$$x = \frac{-(-2) \pm \sqrt{(-2)^2 — 4(1)(-13)}}{2(1)} = \frac{2 \pm \sqrt{4 + 52}}{2} = \frac{2 \pm \sqrt{56}}{2} = \frac{2 \pm 2\sqrt{14}}{2}$$

Получаем два корня:

$$x = 1 + \sqrt{14} \quad \text{или} \quad x = 1 — \sqrt{14}$$

Таким образом, график функции пересекает прямую $y = -10$ в двух точках.