ГДЗ по Алгебре 9 Класс Номер 198 Дорофеев, Суворова — Подробные Ответы

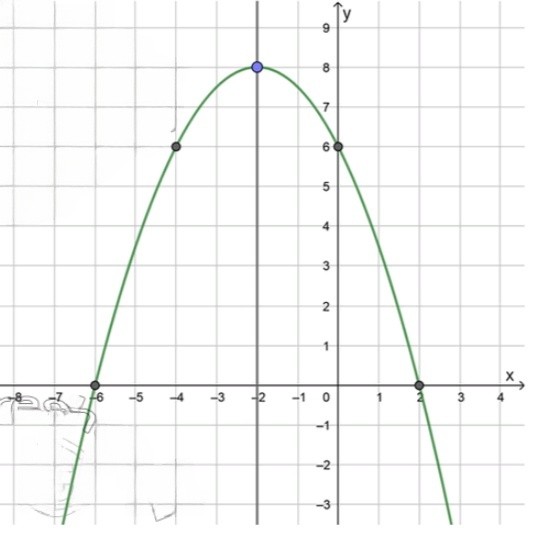
На рисунке 2.6 изображена часть параболы (графика некоторой квадратичной функции) и её ось симметрии. Запишите уравнение оси симетрии.
Перенесите рисунок в тетрадь и достройте параболу. Укажите направление ветвей параболы.
Ответьте на вопросы:
1) Каковы координаты вершины параболы?
2) Чему равно значение у при значении х, равном -4; 1; 3?
3) При каких значениях х значение у равно 0; 3; -3?

Достроим данную параболу для чего:

Выберем на ветви параболы какие-нибудь две точки и отметим на плоскости симметричные им точки, например:
$(-4; 6)$ и $(0; 6)$, $(-6; 0)$ и $(2; 0);$

Проведем вторую ветвь параболы через ее вершину $(-2; 8)$ и через точки $(0; 6)$ и $(2; 0);$

Достроим данную параболу для чего:

Выберем на ветви параболы какие-нибудь две точки и отметим на плоскости симметричные им точки. Пусть на параболе будут точки $(-4; 6)$ и $(0; 6)$, а симметричные им точки будут $(-6; 0)$ и $(2; 0)$.

Для нахождения этих точек и их симметрии, сначала определим уравнение параболы. Пусть у нас есть квадратичное уравнение параболы в виде $y = ax^2 + bx + c$. Для нахождения коэффициентов $a$, $b$, $c$, нужно использовать координаты известных точек. Например, подставим точки $(-4; 6)$ и $(0; 6)$ в уравнение параболы и решим систему уравнений для коэффициентов.

Рассмотрим точку $(0; 6)$, подставим её в уравнение параболы:

$$6 = a(0)^2 + b(0) + c$$ $$c = 6$$

Теперь у нас есть одно уравнение: $y = ax^2 + bx + 6$.

Следующим шагом подставим точку $(-4; 6)$ в уравнение:

$$6 = a(-4)^2 + b(-4) + 6$$ $$6 = 16a — 4b + 6$$

Упростим:

$$16a — 4b = 0$$ $$4a — b = 0 \quad \text{(1)}$$

Далее подставим точку $(2; 0)$:

$$0 = a(2)^2 + b(2) + 6$$ $$0 = 4a + 2b + 6$$

Упростим:

$$4a + 2b = -6$$ $$2a + b = -3 \quad \text{(2)}$$

Теперь решим систему уравнений (1) и (2):

$4a — b = 0$

$2a + b = -3$

Сложим эти два уравнения:

$$4a — b + 2a + b = 0 + (-3)$$ $$6a = -3$$ $$a = -\frac{1}{2}$$

Теперь подставим $a = -\frac{1}{2}$ в уравнение (1):

$$4\left(-\frac{1}{2}\right) — b = 0$$ $$-2 — b = 0$$ $$b = -2$$

Теперь у нас есть полное уравнение параболы:

$$y = -\frac{1}{2}x^2 — 2x + 6$$

Проведем вторую ветвь параболы через её вершину $(-2; 8)$ и через точки $(0; 6)$ и $(2; 0)$.
Вершина параболы находится по формуле $x = \frac{-b}{2a}$. Подставляем $a = -\frac{1}{2}$ и $b = -2$:

$$x = \frac{-(-2)}{2 \cdot \left(-\frac{1}{2}\right)} = \frac{2}{-1} = -2$$

Теперь подставим $x = -2$ в уравнение параболы, чтобы найти $y$:

$$y = -\frac{1}{2}(-2)^2 — 2(-2) + 6 = -\frac{1}{2}(4) + 4 + 6 = -2 + 4 + 6 = 8$$

Таким образом, вершина параболы действительно находится в точке $(-2; 8)$.

Теперь используем симметричные точки для построения второй ветви параболы. Симметричные точки $(0; 6)$ и $(2; 0)$ относятся к первой ветви параболы. Для построения второй ветви, проводим её через вершину $(-2; 8)$ и через эти симметричные точки. Это обеспечивает зеркальное отражение параболы относительно оси симметрии $x = -2$.

Таким образом, парабола будет проходить через точки $(0; 6)$ и $(2; 0)$, а её вторая ветвь будет симметрична первой ветви и будет отражена относительно оси симметрии $x = -2$.