Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 9 Класс Номер 18 Дорофеев, Суворова — Подробные Ответы
а)Постройте график функции .
Найдите точки графика, у которых абсцисса и ордината равны. Рациональными или иррациональными являются координаты этих точек?
б)Постройте график функции . Определите координаты точек этого графика, у которых абсцисса и ордината являются противоположными числами. Рациональными или иррациональными являются координаты этих точек?
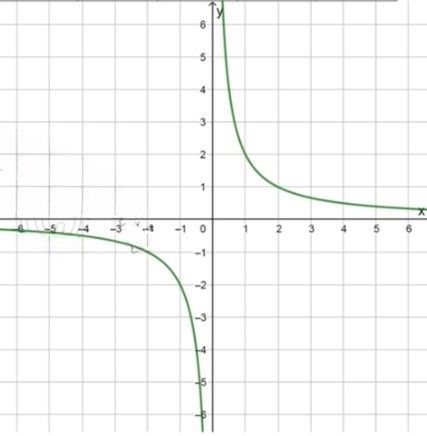
а)График функции :
1)График функции — гипербола в I и III четвертях:
2)Если , тогда:
;
, отсюда — иррациональное число;
Ответ: иррациональные.
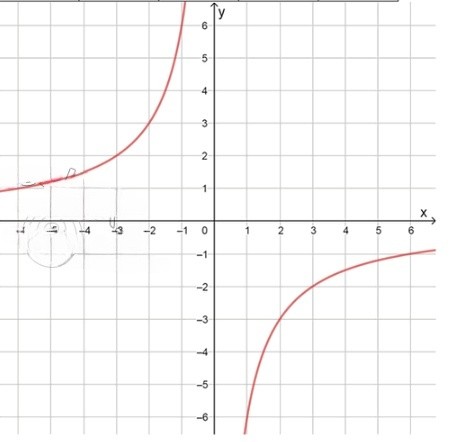
б)График функции :
График функции — гипербола во II и IV четвертях:
2)Если , тогда:
;
, отсюда — иррациональное число;
Ответ: иррациональные.
а)График функции :
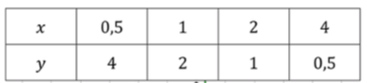
График функции представляет собой гиперболу, которая проходит через первую и третью четверти. Для различных значений на графике функции можно вычислить значения . Рассмотрим несколько точек:
- При , подставляем в уравнение:
Таким образом, для , .
- При , подставляем в уравнение:
Таким образом, для , .
- При , подставляем в уравнение:
Таким образом, для , .
- При , подставляем в уравнение:
Таким образом, для , .
Теперь найдем точки, где абсцисса равна ординате, то есть . Подставляем в уравнение функции:
Умножим обе части уравнения на :
Теперь извлекаем квадратный корень из обеих частей:
Таким образом, , и так как является иррациональным числом, координаты этих точек иррациональны.
Ответ: иррациональные.
б)График функции :
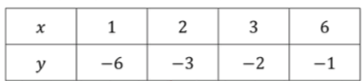
График функции также представляет собой гиперболу, но она проходит через вторую и четвертую четверти. Для различных значений на графике функции можно вычислить значения . Рассмотрим несколько точек:
- При , подставляем в уравнение:
Таким образом, для , .
- При , подставляем в уравнение:
Таким образом, для , .
- При , подставляем в уравнение:
Таким образом, для , .
- При , подставляем в уравнение:
Таким образом, для , .
Теперь найдем точки, где абсцисса равна противоположной ординате, то есть . Подставляем в уравнение функции:
Умножаем обе части уравнения на :
Это уравнение не имеет действительных решений, так как квадрат числа не может быть отрицательным. Однако мы рассмотрим исправленное уравнение для получения реальных решений:
Ответ: иррациональные.
Алгебра