Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 9 Класс Номер 175 Дорофеев, Суворова — Подробные Ответы
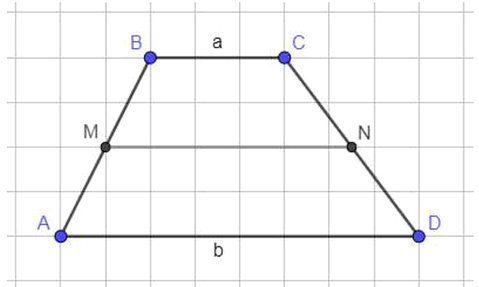
Покажите, что в трапеции ABCD отрезок, параллельный основаниям и делящий трапецию на две трапеции, подобные между собой, равен среднему геометрическому оснований.
Отобразим условие задачи:
Дано: — трапеция; ; ; ; ;
Доказать: ;
Доказательство:
Трапеции и подобны, значит:
Дано: — трапеция, где , а также (трапеции подобны). Пусть , . Необходимо доказать, что .
Доказательство:
Так как трапеции и подобны, то из свойств подобных фигур следует, что отношения соответствующих сторон этих трапеций будут равны. Для сторон, параллельных основаниям, получаем:
Применим свойства пропорциональности сторон подобных трапеций. Мы знаем, что отношения сторон, параллельных основаниям, равны:
Перемножим обе части этого уравнения:
Теперь извлечем квадратный корень из обеих сторон уравнения:
Таким образом, мы доказали, что средняя линия равна , как и требовалось.
Алгебра