ГДЗ по Алгебре 9 Класс Номер 15 Дорофеев, Суворова — Подробные Ответы

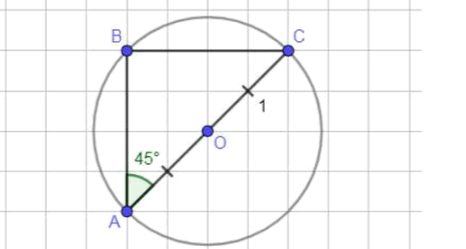
В окружность с центром O и радиусом, равным 1, вписан треугольник (рис. 1.7, а, б).

а) Отобразим условие задачи:

$AC = AO + OC = 2R = 2$ — рациональное число;

Угол $B$ вписан в окружность и опирается на ее диаметр, значит этот угол прямой: $\angle B = 90^\circ$;

По теореме о сумме углов треугольника:

$$\angle C = 180^\circ — \angle B — \angle A = 180^\circ — 90^\circ — 45^\circ = 45^\circ;$$

Таким образом, треугольник $ABC$ — равнобедренный: $AB = CB$;

По теореме Пифагора:

$$A{C}^2=A{B}^2+C{B}^2;$$

$$AC^2 = AB^2 + CB^2;$$ $$2^2=A{B}^2+A{B}^2$$

$$2^2 = AB^2 + AB^2$$ $$2 = 2AB^2, \text{ отсюда } AB = CB = \sqrt{2} \quad \text{— иррациональное число};$$

Ответ: $AC$ — рациональное; $AB$ и $CB$ — иррациональные.

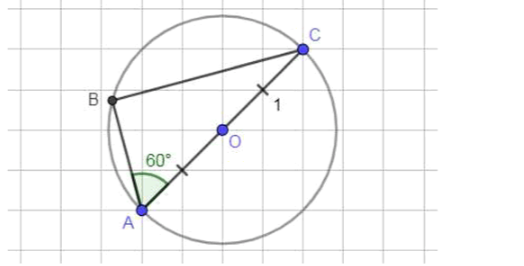
б) Отобразим условие задачи:

$AC = AO + OC = 2R = 2$ — рациональное число;

Угол $B$ вписан в окружность и опирается на ее диаметр, значит этот угол прямой: $\angle B = 90^\circ$;

По теореме о сумме углов треугольника:

$$\angle C = 180^\circ — \angle B — \angle A = 180^\circ — 90^\circ — 60^\circ = 30^\circ;$$

Таким образом, катет $AB$ лежит против угла в $30^\circ$, значит:

$$AB = \frac{1}{2}AC = 1 \quad \text{— рациональное число};$$

По теореме Пифагора:

$$BC = \sqrt{AC^2 — AB^2};$$ $$BC = \sqrt{2^2 — 1^2} = \sqrt{4 — 1} = \sqrt{3} \quad \text{— иррациональное число};$$

Ответ: $AB$ и $AC$ — рациональные; $BC$ — иррациональное.

а) Отобразим условие задачи:

$AC = AO + OC = 2R = 2$ — рациональное число;
Так как радиус окружности $R$ является числом, то длина отрезка $AC$, которая равна $2R$, будет также рациональным числом, так как $R$ умножается на 2, а произведение двух рациональных чисел всегда рационально.

Угол $B$ вписан в окружность и опирается на ее диаметр, значит этот угол прямой: $\angle B = 90^\circ$;
Это важное утверждение, так как согласно теореме о вписанном угле, угол, опирающийся на диаметр окружности, всегда будет прямым (равным $90^\circ$). Это позволяет нам сразу заключить, что $\angle B = 90^\circ$.

По теореме о сумме углов треугольника:
В любом треугольнике сумма углов равна $180^\circ$. В треугольнике $ABC$, имеющем углы $\angle A$, $\angle B$, и $\angle C$, мы знаем, что угол $B$ равен $90^\circ$. Также угол $A$ задан как $45^\circ$. Таким образом, угол $C$ можно найти по формуле:

$$\angle C = 180^\circ — \angle B — \angle A = 180^\circ — 90^\circ — 45^\circ = 45^\circ$$

Таким образом, угол $C$ равен $45^\circ$.

Таким образом, треугольник $ABC$ — равнобедренный: $AB = CB$;
Так как углы $A$ и $C$ равны, а они являются углами при основании треугольника, то треугольник $ABC$ является равнобедренным, и длины его оснований $AB$ и $CB$ равны.

По теореме Пифагора:
Теперь, зная, что треугольник $ABC$ является прямоугольным и равнобедренным, применим теорему Пифагора для нахождения длины катетов $AB$ и $CB$. Пифагорова теорема гласит, что для прямоугольного треугольника сумма квадратов катетов равна квадрату гипотенузы:

$$AC^2 = AB^2 + CB^2$$

Подставляем известные значения:

$$2^2 = AB^2 + AB^2$$

Так как $AB = CB$, выражаем:

$$4 = 2AB^2$$

Разделим обе стороны на 2:

$$2 = AB^2$$

Теперь извлекаем квадратный корень:

$$AB = \sqrt{2}$$

Число $\sqrt{2}$ является иррациональным, так как оно не может быть представлено в виде конечной или периодической десятичной дроби.
Ответ: $AB = CB = \sqrt{2}$, что является иррациональным числом.

Ответ: $AC$ — рациональное; $AB$ и $CB$ — иррациональные.

б) Отобразим условие задачи:

$AC = AO + OC = 2R = 2$ — рациональное число;
Точно так же, как и в пункте (а), длина отрезка $AC$ является рациональным числом, так как $2R = 2$, где $R$ — это радиус окружности, который является рациональным числом.

Угол $B$ вписан в окружность и опирается на ее диаметр, значит этот угол прямой: $\angle B = 90^\circ$;
Это также важное утверждение, так как угол, опирающийся на диаметр окружности, всегда является прямым. Следовательно, $\angle B = 90^\circ$.

По теореме о сумме углов треугольника:
В треугольнике сумма углов равна $180^\circ$. Из этого следует, что угол $C$ можно вычислить, зная углы $A$ и $B$:

$$\angle C = 180^\circ — \angle B — \angle A = 180^\circ — 90^\circ — 60^\circ = 30^\circ$$

Таким образом, угол $C$ равен $30^\circ$.

Таким образом, катет $AB$ лежит против угла в $30^\circ$, значит:
В прямоугольном треугольнике $ABC$ катет, лежащий против угла в $30^\circ$, равен половине гипотенузы $AC$. По теореме о соотношении сторон прямоугольного треугольника, имеющего угол в $30^\circ$, мы имеем:

$$AB = \frac{1}{2}AC = 1$$

Таким образом, $AB = 1$, и это число является рациональным.

По теореме Пифагора:
Для нахождения длины второго катета $BC$ применим теорему Пифагора:

$$BC = \sqrt{AC^2 — AB^2}$$

Подставляем известные значения:

$$BC = \sqrt{2^2 — 1^2} = \sqrt{4 — 1} = \sqrt{3}$$

Число $\sqrt{3}$ является иррациональным, так как оно не может быть представлено в виде конечной или периодической десятичной дроби.
Ответ: $BC = \sqrt{3}$, что является иррациональным числом.

Ответ: $AB$ и $AC$ — рациональные; $BC$ — иррациональное.