Краткий ответ:
а) Функции f ( x ) = 2 x + 1 f(x) = 2x + 1 g ( x ) = x − 3 g(x) = x — 3
1)Обе функции отрицательны:
{ 2 x + 1 < 0 ⇒ { 2 x < − 1 x < − 0.5 x − 3 < 0 ⇒ { x < − 0,5 x < 3 \begin{cases} 2x + 1 < 0 & \Rightarrow \begin{cases} 2x < -1 \\ x < -0.5 \end{cases} \\ x — 3 < 0 & \Rightarrow \begin{cases} x < 3 \end{cases} \end{cases}
x < − 0.5 x < -0.5 x ∈ ( − ∞ ; − 0.5 ) x \in (-\infty; -0.5)
2)Функция f ( x ) f(x) g ( x ) g(x)
{ 2 x + 1 > 0 ⇒ { 2 x > − 1 x > − 0.5 x − 3 < 0 ⇒ { x > − 0,5 x < 3 \begin{cases} 2x + 1 > 0 & \Rightarrow \begin{cases} 2x > -1 \\ x > -0.5 \end{cases} \\ x — 3 < 0 & \Rightarrow \begin{cases} x < 3 \end{cases} \end{cases}
− 0.5 < x < 3 -0.5 < x < 3 x ∈ ( − 0.5 ; 3 ) x \in (-0.5; 3)
3)Функция g ( x ) g(x) f ( x ) f(x)
{ 2 x + 1 < 0 ⇒ { 2 x < − 1 x < − 0.5 x − 3 > 0 ⇒ { x < − 0,5 x > 3 \begin{cases} 2x + 1 < 0 & \Rightarrow \begin{cases} 2x < -1 \\ x < -0.5 \end{cases} \\ x — 3 > 0 & \Rightarrow \begin{cases} x > 3 \end{cases} \end{cases}
Таких значений аргумента не существует;
4)Обе функции положительны:
{ 2 x + 1 > 0 ⇒ { 2 x > − 1 x > − 0.5 x − 3 > 0 ⇒ { x > − 0,5 x > 3 \begin{cases} 2x + 1 > 0 & \Rightarrow \begin{cases} 2x > -1 \\ x > -0.5 \end{cases} \\ x — 3 > 0 & \Rightarrow \begin{cases} x > 3 \end{cases} \end{cases}
x > 3 x > 3 x ∈ ( 3 ; + ∞ ) x \in (3; +\infty)
5)y = 2 x + 1 y = 2x + 1
6)y = x − 3 y = x — 3
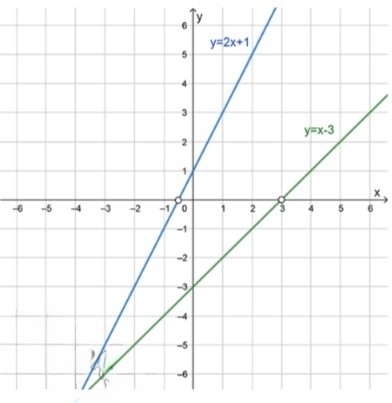
7)График функций:
б) Функции f ( x ) = − 1 2 x + 1 f(x) = -\frac{1}{2}x + 1 g ( x ) = 1 2 x − 2 g(x) = \frac{1}{2}x — 2
1)Обе функции отрицательны:
{ − 0.5 x + 1 < 0 ⇒ { − 0.5 x < − 1 x > 2 0.5 x − 2 < 0 ⇒ { x > 2 x < 4 \begin{cases} -0.5x + 1 < 0 & \Rightarrow \begin{cases} -0.5x < -1 \\ x > 2 \end{cases} \\ 0.5x — 2 < 0 & \Rightarrow \begin{cases} 0.5x < 2 \\ x < 4 \end{cases} \end{cases}
2 < x < 4 2 < x < 4 x ∈ ( 2 ; 4 ) x \in (2; 4)
2)Функция f ( x ) f(x) g ( x ) g(x)
{ − 0.5 x + 1 > 0 ⇒ { − 0.5 x > − 1 x < 2 0.5 x − 2 < 0 ⇒ { x < 2 x < 4 \begin{cases} -0.5x + 1 > 0 & \Rightarrow \begin{cases} -0.5x > -1 \\ x < 2 \end{cases} \\ 0.5x — 2 < 0 & \Rightarrow \begin{cases} 0.5x < 2 \\ x < 4 \end{cases} \end{cases}
x < 2 x < 2 x ∈ ( − ∞ ; 2 ) x \in (-\infty; 2)
3)Функция g ( x ) g(x) f ( x ) f(x)
{ − 0.5 x + 1 < 0 ⇒ { − 0.5 x < − 1 x > 2 0.5 x − 2 > 0 ⇒ { x < 2 x > 4 \begin{cases} -0.5x + 1 < 0 & \Rightarrow \begin{cases} -0.5x < -1 \\ x > 2 \end{cases} \\ 0.5x — 2 > 0 & \Rightarrow \begin{cases} 0.5x > 2 \\ x > 4 \end{cases} \end{cases}
x > 4 x > 4 x ∈ ( 4 ; + ∞ ) x \in (4; +\infty)
4)Обе функции положительны:
{ − 0.5 x + 1 > 0 ⇒ { − 0.5 x > − 1 x < 2 0.5 x − 2 > 0 ⇒ { x < 2 x > 4 \begin{cases} -0.5x + 1 > 0 & \Rightarrow \begin{cases} -0.5x > -1 \\ x < 2 \end{cases} \\ 0.5x — 2 > 0 & \Rightarrow \begin{cases} 0.5x > 2 \\ x > 4 \end{cases} \end{cases}
Таких значений аргумента не существует;
5)y = − 0.5 x + 1 y = -0.5x + 1
6)y = 0.5 x − 2 y = 0.5x — 2
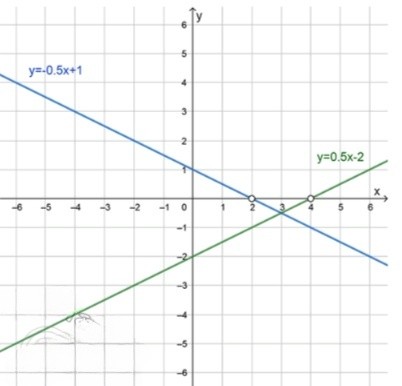
7)График функций:
Подробный ответ:
а) Функции f ( x ) = 2 x + 1 f(x) = 2x + 1 g ( x ) = x − 3 g(x) = x — 3
Обе функции отрицательны:
{ 2 x + 1 < 0 x − 3 < 0 \begin{cases} 2x + 1 < 0 \\ x — 3 < 0 \end{cases}
Решим первое неравенство 2 x + 1 < 0 2x + 1 < 0
Прибавим 1 к обеим частям:
2 x < − 1 2x < -1
Разделим обе части на 2:
x < − 0.5. x < -0.5.
Решим второе неравенство x − 3 < 0 x — 3 < 0
x < 3. x < 3.
Объединяем оба неравенства:
x < − 0.5 или x ∈ ( − ∞ ; − 0.5 ) . x < -0.5 \quad \text{или} \quad x \in (-\infty; -0.5).
Функция f ( x ) f(x) g ( x ) g(x)
{ 2 x + 1 > 0 x − 3 < 0 \begin{cases} 2x + 1 > 0 \\ x — 3 < 0 \end{cases}
Решим первое неравенство 2 x + 1 > 0 2x + 1 > 0
Прибавим 1 к обеим частям:
2 x > − 1 2x > -1
Разделим обе части на 2:
x > − 0.5. x > -0.5.
Решим второе неравенство x − 3 < 0 x — 3 < 0
x < 3. x < 3.
Объединяем оба неравенства:
− 0.5 < x < 3 или x ∈ ( − 0.5 ; 3 ) . -0.5 < x < 3 \quad \text{или} \quad x \in (-0.5; 3).
Функция g ( x ) g(x) f ( x ) f(x)
{ 2 x + 1 < 0 x − 3 > 0 \begin{cases} 2x + 1 < 0 \\ x — 3 > 0 \end{cases}
Решим первое неравенство 2 x + 1 < 0 2x + 1 < 0
Прибавим 1 к обеим частям:
2 x < − 1 2x < -1
Разделим обе части на 2:
x < − 0.5. x < -0.5.
Решим второе неравенство x − 3 > 0 x — 3 > 0
x > 3. x > 3.
Так как x x − 0.5 -0.5
Обе функции положительны:
{ 2 x + 1 > 0 x − 3 > 0 \begin{cases} 2x + 1 > 0 \\ x — 3 > 0 \end{cases}
Решим первое неравенство 2 x + 1 > 0 2x + 1 > 0
Прибавим 1 к обеим частям:
2 x > − 1 2x > -1
Разделим обе части на 2:
x > − 0.5. x > -0.5.
Решим второе неравенство x − 3 > 0 x — 3 > 0
x > 3. x > 3.
Объединяем оба неравенства:
x > 3 или x ∈ ( 3 ; + ∞ ) . x > 3 \quad \text{или} \quad x \in (3; +\infty).
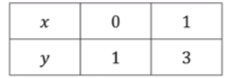
y = 2 x + 1 y = 2x + 1
Для x = 0 x = 0
y = 2 ⋅ 0 + 1 = 1. y = 2 \cdot 0 + 1 = 1.
Для x = 1 x = 1
y = 2 ⋅ 1 + 1 = 3. y = 2 \cdot 1 + 1 = 3.
Таблица значений:
\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & 1 & 3 \\ \hline \end{array} y = x − 3 y = x — 3
Для x = 2 x = 2
y = 2 − 3 = − 1. y = 2 — 3 = -1.
Для x = 3 x = 3
y = 3 − 3 = 0. y = 3 — 3 = 0.
Таблица значений:
\begin{array}{|c|c|c|} \hline x & 2 & 3 \\ \hline y & -1 & 0 \\ \hline \end{array}
б) Функции f ( x ) = − 1 2 x + 1 f(x) = -\frac{1}{2}x + 1 g ( x ) = 1 2 x − 2 g(x) = \frac{1}{2}x — 2
Обе функции отрицательны:
{ − 1 2 x + 1 < 0 1 2 x − 2 < 0 \begin{cases} -\frac{1}{2}x + 1 < 0 \\ \frac{1}{2}x — 2 < 0 \end{cases}
Решим первое неравенство − 1 2 x + 1 < 0 -\frac{1}{2}x + 1 < 0
Вычитаем 1 из обеих частей:
− 1 2 x < − 1. -\frac{1}{2}x < -1.
Умножаем обе части на -2 (при этом знак неравенства меняется):
x > 2. x > 2.
Решим второе неравенство 1 2 x − 2 < 0 \frac{1}{2}x — 2 < 0
Прибавим 2 к обеим частям:
1 2 x < 2. \frac{1}{2}x < 2.
Умножаем обе части на 2:
x < 4. x < 4.
Объединяем оба неравенства:
2 < x < 4 или x ∈ ( 2 ; 4 ) . 2 < x < 4 \quad \text{или} \quad x \in (2; 4).
Функция f ( x ) f(x) g ( x ) g(x)
{ − 1 2 x + 1 > 0 1 2 x − 2 < 0 \begin{cases} -\frac{1}{2}x + 1 > 0 \\ \frac{1}{2}x — 2 < 0 \end{cases}
Решим первое неравенство − 1 2 x + 1 > 0 -\frac{1}{2}x + 1 > 0
Вычитаем 1 из обеих частей:
− 1 2 x > − 1. -\frac{1}{2}x > -1.
Умножаем обе части на -2 (при этом знак неравенства меняется):
x < 2. x < 2.
Решим второе неравенство 1 2 x − 2 < 0 \frac{1}{2}x — 2 < 0
Прибавим 2 к обеим частям:
1 2 x < 2. \frac{1}{2}x < 2.
Умножаем обе части на 2:
x < 4. x < 4.
Объединяем оба неравенства:
x < 2 или x ∈ ( − ∞ ; 2 ) . x < 2 \quad \text{или} \quad x \in (-\infty; 2).
Функция g ( x ) g(x) f ( x ) f(x)
{ − 1 2 x + 1 < 0 1 2 x − 2 > 0 \begin{cases} -\frac{1}{2}x + 1 < 0 \\ \frac{1}{2}x — 2 > 0 \end{cases}
Решим первое неравенство − 1 2 x + 1 < 0 -\frac{1}{2}x + 1 < 0
Вычитаем 1 из обеих частей:
− 1 2 x < − 1. -\frac{1}{2}x < -1.
Умножаем обе части на -2 (при этом знак неравенства меняется):
x > 2. x > 2.
Решим второе неравенство 1 2 x − 2 > 0 \frac{1}{2}x — 2 > 0
Прибавим 2 к обеим частям:
1 2 x > 2. \frac{1}{2}x > 2.
Умножаем обе части на 2:
x > 4. x > 4.
Объединяем оба неравенства:
x > 4 или x ∈ ( 4 ; + ∞ ) . x > 4 \quad \text{или} \quad x \in (4; +\infty).
Обе функции положительны:
{ − 1 2 x + 1 > 0 1 2 x − 2 > 0 \begin{cases} -\frac{1}{2}x + 1 > 0 \\ \frac{1}{2}x — 2 > 0 \end{cases}
Решим первое неравенство − 1 2 x + 1 > 0 -\frac{1}{2}x + 1 > 0
Вычитаем 1 из обеих частей:
− 1 2 x > − 1. -\frac{1}{2}x > -1.
Умножаем обе части на -2 (при этом знак неравенства меняется):
x < 2. x < 2.
Решим второе неравенство 1 2 x − 2 > 0 \frac{1}{2}x — 2 > 0
Прибавим 2 к обеим частям:
1 2 x > 2. \frac{1}{2}x > 2.
Умножаем обе части на 2:
x > 4. x > 4.
Так как нет таких значений x x
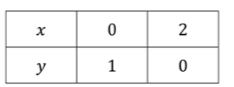
y = − 0.5 x + 1 y = -0.5x + 1
Для x = 0 x = 0
y = − 0.5 ⋅ 0 + 1 = 1. y = -0.5 \cdot 0 + 1 = 1.
Для x = 2 x = 2
y = − 0.5 ⋅ 2 + 1 = 0. y = -0.5 \cdot 2 + 1 = 0.
Таблица значений:
\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 1 & 0 \\ \hline \end{array} y = 0.5 x − 2 y = 0.5x — 2
Для x = 0 x = 0
y = 0.5 ⋅ 0 − 2 = − 2. y = 0.5 \cdot 0 — 2 = -2.
Для x = 2 x = 2
y = 0.5 ⋅ 2 − 2 = − 1. y = 0.5 \cdot 2 — 2 = -1.
Таблица значений:
\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & -2 & -1 \\ \hline \end{array}