ГДЗ по Алгебре 9 Класс Номер 120 Дорофеев, Суворова — Подробные Ответы

1)Найдите промежуток, на котором функции $y = -2x + 4$ и $y = \frac{1}{2}x + 2$ одновременно принимают положительные значения. Начертите в одной системе координат графики этих функций и отметьте на оси $x$ соответствующий промежуток.

2)Укажите какое-нибудь значение аргумента, не принадлежащее отмеченному промежутку, и определите знак каждой из функций при этом значении.

3)Существуют ли значения аргумента, при которых обе функции отрицательны? Проверьте свой ответ, решив систему неравенств.

Функции: $y = -2x + 4$ и $y = \frac{1}{2}x + 2$.

1. Обе функции принимают положительные значения:

$$\begin{cases} -2x + 4 > 0 \\ \frac{1}{2}x + 2 > 0 \end{cases} \Rightarrow \begin{cases} -2x > -4 \\ 0.5x > -2 \end{cases} \Rightarrow \begin{cases} x < 2 \\ x > -4 \end{cases}$$

$-4 < x < 2$ или $x \in (-4; 2)$.

$y = -2x + 4$ — уравнение прямой:

$$\overline{)\begin{array}{ccc}\mathrm{<a\; href="https://gdz-dorofeev.ru/wp-content/uploads/gdz-dorofeev.ru/2025/07/2025-07-06\_16-37-25.png"><img\; decoding="async"\; class="aligncenter\; size-full\; wp-image-20185"\; src="data:image/svg+xml,\%3Csvg\%20xmlns=\text{'}http://www.w3.org/2000/svg\text{'}\%20viewBox=\text{'}0\%200\%20224\%2078\text{'}\%3E\%3C/svg\%3E"\; alt=""\; width="224"\; height="78"\; data-lazy-src="https://gdz-dorofeev.ru/wp-content/uploads/gdz-dorofeev.ru/2025/07/2025-07-06\_16-37-25.png"></a>}& & \\ & & \end{array}}$$2) $y = 0.5x + 2$ — уравнение прямой:

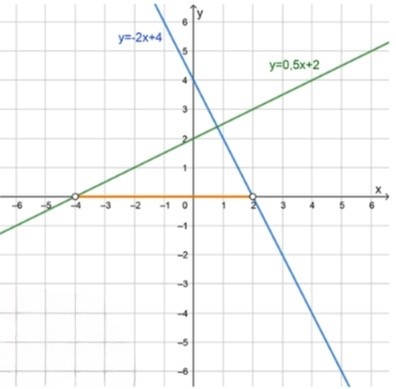
$$\overline{)\begin{array}{c}\end{array}}$$ \begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 3 \\ \hline \end{array}3)График функций:

(Графики приведены на рисунке.)

2. Значение аргумента, не принадлежащее этому промежутку:

Пусть $x = 7$, тогда:

$$y=-2x+4=-2\cdot 7+4=-14+4=-10<0;$$

$$y = -2x + 4 = -2 \cdot 7 + 4 = -14 + 4 = -10 < 0;$$ $$y = 0.5x + 2 = 0.5 \cdot 7 + 2 = 3.5 + 2 = 5.5 > 0;$$

3. Обе функции принимают отрицательные значения:

$$\begin{cases} -2x + 4 \leq 0 \\ \frac{1}{2}x + 2 < 0 \end{cases} \Rightarrow \begin{cases} -2x \leq -4 \\ 0.5x < -2 \end{cases} \Rightarrow \begin{cases} x \geq 2 \\ x < -4 \end{cases}$$

Такого значения аргумента не существует.

Обе функции принимают положительные значения:

Рассмотрим систему неравенств:

$$\begin{cases} -2x + 4 > 0 \\ \frac{1}{2}x + 2 > 0 \end{cases}$$

Первое неравенство: $-2x + 4 > 0$

Прибавим 2x к обеим частям неравенства:

$$4 > 2x.$$

Разделим обе части на 2:

$$2 > x \quad \text{или} \quad x < 2.$$

Второе неравенство: $\frac{1}{2}x + 2 > 0$

Вычитаем 2 из обеих частей:

$$\frac{1}{2}x > -2.$$

Умножаем обе части на 2:

$$x > -4.$$

Теперь объединим результаты двух неравенств:

$$x < 2 \quad \text{и} \quad x > -4.$$

Таким образом, решениями этой системы будут все значения $x$ в интервале $(-4; 2)$, то есть:

$$x \in (-4; 2).$$

Таблицы значений функций:

Для функции $y = -2x + 4$ при $x = 0$ и $x = 2$:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 4 & 0 \\ \hline \end{array}$$Для функции $y = \frac{1}{2}x + 2$ при $x = 0$ и $x = 2$:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 3 \\ \hline \end{array}$$Графики функций:

Значение аргумента, не принадлежащее этому промежутку:

Пусть $x = 7$. Тогда для первой функции $y = -2x + 4$:

$$y = -2 \cdot 7 + 4 = -14 + 4 = -10 < 0.$$

Для второй функции $y = \frac{1}{2}x + 2$:

$$y = 0.5 \cdot 7 + 2 = 3.5 + 2 = 5.5 > 0.$$

Таким образом, при $x = 7$, первая функция отрицательна, а вторая — положительна.

Обе функции принимают отрицательные значения:

Рассмотрим систему неравенств:

$$\begin{cases} -2x + 4 \leq 0 \\ \frac{1}{2}x + 2 < 0 \end{cases}$$

Первое неравенство: $-2x + 4 \leq 0$

Прибавим $2x$ к обеим частям:

$$4 \leq 2x.$$

Разделим обе части на 2:

$$2 \leq x \quad \text{или} \quad x \geq 2.$$

Второе неравенство: $\frac{1}{2}x + 2 < 0$

Вычитаем 2 из обеих частей:

$$\frac{1}{2}x < -2.$$

Умножаем обе части на 2:

$$x < -4.$$

Теперь объединяем результаты двух неравенств:

$$x \geq 2 \quad \text{и} \quad x < -4.$$

Так как нет таких значений $x$, которые одновременно удовлетворяют обоим неравенствам, то решений этой системы не существует.