ГДЗ по Алгебре 8 Класс Номер 896 Дорофеев, Суворова — Подробные Ответы

Фишку наугад бросают в квадрат со стороной 1, и она попадает в некоторую точку M. Какова вероятность того, что:
а) расстояние от точки M до ближайшей стороны квадрата не превосходит 0,25;
б) расстояние от точки M до ближайшей диагонали квадрата не превосходит 0,25

а) Рисунок:

Площадь всего квадрата равна 1.
Площадь незакрашенного квадрата равна 0,25.

Вероятность равна:
$P = \frac{1 — 0,25}{1} = \frac{0,75}{1} = 0,75$.

Ответ: $\frac{3}{4}$.

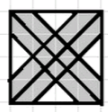
б) Рисунок:

Площадь всего квадрата равна 1.
Площадь оставшейся части равна:
$\left( 1 — \frac{1}{\sqrt{2}} \right)^2 = 1 — 2 \cdot \frac{1}{\sqrt{2}} + \frac{1}{2} = \frac{3}{2} — \frac{2}{\sqrt{2}} = \frac{3}{2} — \frac{2\sqrt{2}}{2} = \frac{3 — 2\sqrt{2}}{2}$.

Вероятность равна:
$1 — \frac{3 — 2\sqrt{2}}{2} = \frac{2 — (3 — 2\sqrt{2})}{2} = \frac{2 — 3 + 2\sqrt{2}}{2} = \frac{2\sqrt{2} — 1}{2}$.

Ответ: $\frac{2\sqrt{2} — 1}{2}$.

а) Рисунок:

Площадь всего квадрата равна 1.
Площадь незакрашенного квадрата равна 0,25.

Для начала определим вероятность попасть в закрашенную часть квадрата. Площадь всего квадрата, как указано, равна 1. Площадь незакрашенного квадрата составляет 0,25. Чтобы вычислить площадь закрашенной части, нужно из площади всего квадрата вычесть площадь незакрашенного квадрата. Это делаем следующим образом:

$$S_{\text{закрашенная}} = S_{\text{весь}} — S_{\text{незакрашенная}} = 1 — 0,25 = 0,75$$

Теперь, вероятность попасть в закрашенную часть фигуры равна отношению площади закрашенной части к площади всего квадрата. Площадь всего квадрата равна 1, поэтому вероятность будет вычисляться как:

$$P = \frac{S_{\text{закрашенная}}}{S_{\text{весь}}} = \frac{0,75}{1} = 0,75$$

Таким образом, вероятность попасть в закрашенную часть квадрата составляет $\frac{3}{4}$.

Ответ: $\frac{3}{4}$.

б) Рисунок:

Площадь всего квадрата равна 1.
Площадь оставшейся части равна:

Для начала найдем площадь оставшейся части. В формуле для площади оставшейся части присутствует выражение $1 — \frac{1}{\sqrt{2}}$, что означает, что нужно вычислить квадрат разности. Мы вычисляем квадрат следующего выражения:

$$\left( 1 — \frac{1}{\sqrt{2}} \right)^2$$

Раскроем квадрат, используя формулу для квадрата разности $(a — b)^2 = a^2 — 2ab + b^2$, где $a = 1$ и $b = \frac{1}{\sqrt{2}}$:

$$\left( 1 — \frac{1}{\sqrt{2}} \right)^2 = 1^2 — 2 \cdot 1 \cdot \frac{1}{\sqrt{2}} + \left( \frac{1}{\sqrt{2}} \right)^2$$

Вычислим каждое из слагаемых:

$$1^2 = 1, \quad 2 \cdot 1 \cdot \frac{1}{\sqrt{2}} = \frac{2}{\sqrt{2}} = \sqrt{2}, \quad \left( \frac{1}{\sqrt{2}} \right)^2 = \frac{1}{2}$$

Теперь подставим все значения:

$$\left( 1 — \frac{1}{\sqrt{2}} \right)^2 = 1 — \sqrt{2} + \frac{1}{2}$$

Приводим к общему знаменателю:

$$1 = \frac{2}{2}, \quad \frac{2}{2} — \sqrt{2} + \frac{1}{2} = \frac{3}{2} — \sqrt{2}$$

Таким образом, площадь оставшейся части равна:

$$\frac{3}{2} — \sqrt{2}$$

Теперь, для нахождения вероятности, вычитаем эту площадь из площади всего квадрата, которая равна 1:

$$P = 1 — \left( \frac{3}{2} — \sqrt{2} \right)$$

Раскроем скобки:

$$P = 1 — \frac{3}{2} + \sqrt{2}$$

Приводим к общему знаменателю:

$$1 = \frac{2}{2}, \quad \frac{2}{2} — \frac{3}{2} + \sqrt{2} = \frac{-1}{2} + \sqrt{2}$$

Ответ: $\frac{2\sqrt{2} — 1}{2}$.