ГДЗ по Алгебре 8 Класс Номер 856 Это Надо Знать Дорофеев, Суворова — Подробные Ответы

1. Задайте формулой зависимость объёма куба $V$ от длины его ребра $a$. Какая переменная в этом примере является функцией, а какая — аргументом? Укажите область определения данной функции.
2. Используя текст учебника, приведите примеры задания функции графиком, таблицей, формулой.
3. Прочитайте запись $f(x) = x + 3$. Что означает запись $f(-5)$? Найдите $f(-5)$.
4. На примере функции $y = \frac{5}{x-1}$ объясните, как находят область определения функции, заданной формулой.
5. На рисунке 5.60 изображён график функции, заданной на промежутке $[-5; 5]$. По графику определите:
   а) значение $y$ при $x = -1$; $0$; $3$;
   б) значения $x$, при которых $y = 0$; $1$; $-1$.
6. С помощью графика (рис. 5.60) опишите её свойства.
7. Сформулируйте определение линейной функции. Приведите пример конкретной формулы, задающей линейную функцию.
8. Что является графиком линейной функции?
9. При каких значениях $k$ функция $y = kx + 1$ является возрастающей/убывающей? Приведите пример возрастающей линейной функции; убывающей линейной функции. В каждом случае изобразите схематически её график.
10. Укажите область определения функции $y = \frac{k}{x}$. Что является графиком функции $y = \frac{k}{x}$?
11. Как расположен на координатной плоскости график функции $y = \frac{k}{x}$ при $k > 0$ и при $k < 0$?

$\mathrm{1.\; V}=a^3$,
где $a$ – аргумент, $V$ – функция.
Область определения функции: $a>0$.

2. Задание функции графиком:

Задание функции таблицей:

$$\overline{)\begin{array}{cccccc}x& -2& -1& 0& 1& 2\\ y& 4& 1& 0& 1& 4\end{array}}$$

Задание функции формулой:
$y=x^2$.

$\mathrm{3.\; f}(x)=x+3$.
$f(-5)$ означает значение функции при $x=-5$.
$f(-5)=-5+3=-2$.

$\mathrm{4.\; y}=\frac{5}{x-1}$
$x-1\mathrm{\ne }0$
$x\mathrm{\ne }1$.
Ответ: все числа, кроме 1.

5. a) при $x=-1$, $y=3,1$;
при $x=0$, $y=2$;
при $x=3$, $y=-1$.

b) при $y=0$, $x=-4,1$ и $x=2$;
при $y=1$, $x=-3,7$ и $x=1$;
при $y=-1$, $x=-4,7$ и $x=3$.

6. Область определения функции: $[-5;5]$.

$y=0$, при $x=-4,1$ и $x=2$.

$y>0$ при $x\in (-4,1)$; $y<0$ при $x\in [-5;-4,1)$ и $(2;5]$.

функция возрастает при $x\in [-5;-2]$;
функция убывает при $x\in [-2;5]$.

7. Функция, которую можно задать формулой вида $y=kx+l$, где $k$ и $l$ – некоторые числа, называется линейной.
Например: $y=2x+5$.

8. Графиком линейной функции является прямая.

$\mathrm{9.\; y}=kx+l$;
при $k>0$ – функция возрастающая;
при $k<0$ – функция убывающая.
Пример возрастающей линейной функции: $y=0,5x+4$;

Пример убывающей линейной функции: $y=-\frac{1}{3}x-3$.

$\mathrm{10.\; y}=\frac{k}{x}$, область определения функции: $x\mathrm{\ne }0$.
Графиком данной функции является гипербола.

$\mathrm{11.\; y}=\frac{k}{x}$,
при $k>0$ – в первой и третьей четвертях;
при $k<0$ – во второй и четвертой четвертях.

$\mathrm{1.\; V}=a^3$,
где $a$ – аргумент, $V$ – функция.
Область определения функции: $a>0$.

В этом примере мы имеем функцию $V=a^3$, где $a$ является переменной. Функция возводит аргумент $a$ в третью степень, что означает, что $V$ будет зависеть от $a$, и его значение будет определяться как куб аргумента.

Область определения функции $a>0$ ограничивает возможные значения переменной $a$, что означает, что функция определена только для положительных значений $a$. Это условие исключает ноль и все отрицательные числа.

2. Задание функции графиком:

Задание функции таблицей:

$$\overline{)\begin{array}{cccccc}x& -2& -1& 0& 1& 2\\ y& 4& 1& 0& 1& 4\end{array}}$$

Задание функции формулой:
$y=x^2$.

В данном примере функция представлена тремя способами: графически, таблицей значений и формулой.

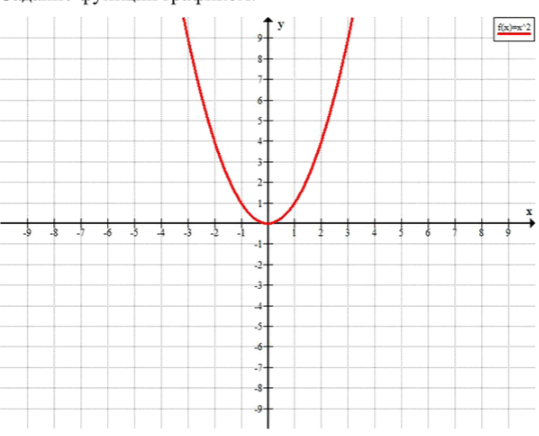
График функции $y=x^2$ будет параболой, открывающейся вверх, с вершиной в начале координат.

Таблица значений показывает, как функция принимает различные значения $y$ в зависимости от значения $x$. Например, когда $x=0$, $y=0$, а когда $x=2$, $y=4$. Эти значения соответствуют точкам на графике функции $y=x^2$.

Формула $y=x^2$ описывает математически, как значение $y$ вычисляется через $x$. Это основная форма функции, которая определяет зависимость между переменными.

$\mathrm{3.\; f}(x)=x+3$.
$f(-5)$ означает значение функции при $x=-5$.
$f(-5)=-5+3=-2$.

В данном примере функция линейная и представлена формулой $f(x)=x+3$. Это означает, что для любого значения $x$ функция $f(x)$ прибавляет 3 к $x$. Чтобы найти значение функции при $x=-5$, подставляем это значение в формулу:

$$f(-5)=-5+3=-2$$

Это означает, что при $x=-5$ значение функции $f(x)$ равно $-2$.

$\mathrm{4.\; y}=\frac{5}{x-1}$
$x-1\mathrm{\ne }0$
$x\mathrm{\ne }1$.
Ответ: все числа, кроме 1.

Здесь мы имеем дробную функцию, которая зависит от $x$. Важно заметить, что знаменатель не может быть равен нулю, так как деление на ноль невозможно. Условие $x-1\mathrm{\ne }0$ приводит к ограничению на значение $x$, и из этого следует, что $x\mathrm{\ne }1$. Таким образом, функция определена для всех значений $x$, кроме $x=1$.

5. a) при $x=-1$, $y=3,1$;
при $x=0$, $y=2$;
при $x=3$, $y=-1$.

б) при $y=0$, $x=-4,1$ и $x=2$;
при $y=1$, $x=-3,7$ и $x=1$;
при $y=-1$, $x=-4,7$ и $x=3$.

Этот пример описывает два случая, где даны значения $x$ и $y$, и нужно найти соответствующие значения переменных.

a) Заданы значения $x$, и нужно найти $y$ для каждого из них. Например, при $x=-1$, $y=3,1$, при $x=0$, $y=2$, и так далее.

б) Заданы значения $y$, и нужно найти $x$ для каждого из них. Например, при $y=0$, $x=-4,1$ и $x=2$, при $y=1$, $x=-3,7$ и $x=1$, и так далее.

6. Область определения функции: $[-5;5]$.

$y=0$, при $x=-4,1$ и $x=2$.

$y>0$ при $x\in (-4,1)$; $y<0$ при $x\in [-5;-4,1)$ и $(2;5]$.

функция возрастает при $x\in [-5;-2]$;
функция убывает при $x\in [-2;5]$.

В этом примере мы анализируем свойства функции. Область определения функции ограничена интервалом $[-5;5]$, что означает, что функция принимает значения только в этом интервале. Также даны интервалы, на которых функция принимает положительные и отрицательные значения, а также на которых функция возрастает и убывает.

7. Функция, которую можно задать формулой вида $y=kx+l$, где $k$ и $l$ – некоторые числа, называется линейной.
Например: $y=2x+5$.

Линейная функция – это функция, график которой представляет собой прямую. Формула линейной функции имеет вид $y=kx+l$, где $k$ – угловой коэффициент, а $l$ – свободный член. Угловой коэффициент $k$ определяет наклон прямой, а свободный член $l$ определяет точку пересечения прямой с осью $y$.

8. Графиком линейной функции является прямая.

График линейной функции всегда является прямой линией, так как она описывает зависимость между двумя переменными, где изменение одной переменной приводит к пропорциональному изменению другой. Наклон прямой зависит от значения углового коэффициента $k$, а точка пересечения с осью $y$ зависит от значения свободного члена $l$.

$\mathrm{9.\; y}=kx+l$;
при $k>0$ – функция возрастающая;
при $k<0$ – функция убывающая.
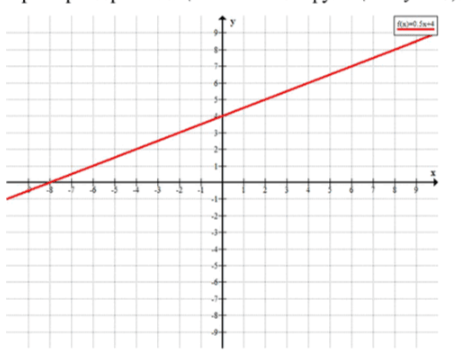
Пример возрастающей линейной функции: $y=0,5x+4$;

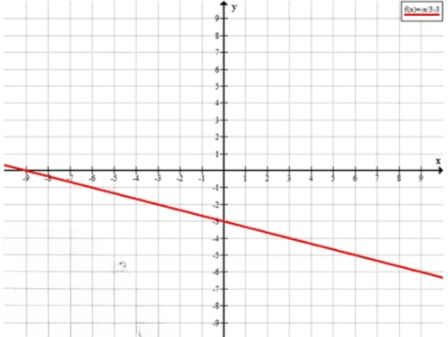
Пример убывающей линейной функции: $y=-\frac{1}{3}x-3$.

Если угловой коэффициент $k$ положительный, то прямая функция возрастает, то есть её график поднимается вверх слева направо. Если $k$ отрицательный, то функция убывает, то есть график функции наклоняется вниз слева направо.

$\mathrm{10.\; y}=\frac{k}{x}$, область определения функции: $x\mathrm{\ne }0$.
Графиком данной функции является гипербола.

Это пример гиперболической функции, где значение функции зависит от обратного значения $x$. Область определения функции ограничена тем, что $x\mathrm{\ne }0$, так как деление на ноль невозможно. График такой функции представляет собой гиперболу, которая имеет две ветви, одну в первой и третьей четвертях, а другую во второй и четвертой.

$\mathrm{11.\; y}=\frac{k}{x}$,
при $k>0$ – в первой и третьей четвертях;
при $k<0$ – во второй и четвертой четвертях.

График функции $y=\frac{k}{x}$ зависит от знака $k$. Если $k>0$, то обе ветви гиперболы находятся в первой и третьей четвертях. Если $k<0$, то ветви гиперболы будут находиться во второй и четвертой четвертях.