Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 856 Это Надо Уметь Дорофеев, Суворова — Подробные Ответы
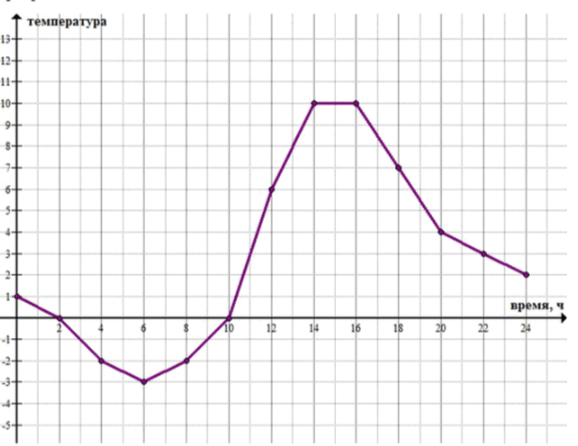
1. В таблице приведены данные температуры воздуха 10 апреля в городе Грибове:
Постройте график температуры и определите:
а) в какое время суток температура равнялась ;
б) в какое время суток температура возрастала; убывала; была положительной; была отрицательной;
в) каково максимальное значение температуры, каково её минимальное значение;
г) в каких границах менялась температура в течение суток;
д) чему равнялась температура в ч;
е) в какое время суток температура равнялась .
2. Функция задана формулой .
а) Найдите значение функции при ; .
б) При каких значениях значение функции равно ?
3. Функция задана формулой .
а) Найдите , .
б) Найдите , при котором ; .
4. Определите нули функции .
5. По графику функции (см. рис. 5.30) определите:
а) нули функции;
б) значения аргумента, при которых функция положительна;
в) промежуток, на котором функция убывает;
г) наибольшее значение функции.
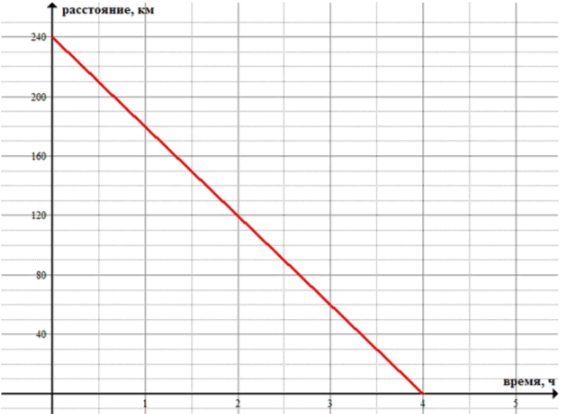
6. От Москвы до Ржева км. Автобус выходит из Москвы и едет во Ржев со средней скоростью км/ч. Расстояние , которое остаётся проехать до Ржева, — это функция времени движения автобуса.
а) Задайте эту функцию формулой.
б) Какое расстояние останется проехать автобусу через час после начала движения? через ч? через ч?
в) Через какое время автобус будет находиться в км от Ржева? в км от Ржева?
г) Что является графиком данной функции?
д) Возрастающей или убывающей является функция?
е) Постройте график данной функции (выберите удобные единицы на осях).
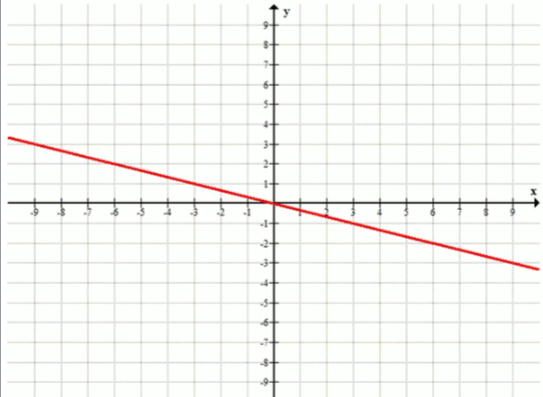
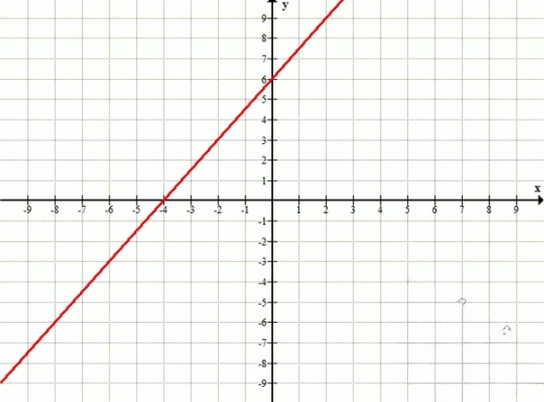
7. Постройте график функции:
а) ;
б) ;
в) .
8. Постройте график функции и ответьте на вопросы:
а) При каких значениях значения функции равны ? больше ? меньше ?
б) Возрастающей или убывающей является функция?
9. Постройте график функции .
а) Укажите область определения этой функции.
б) При каких значениях значения функции больше нуля? меньше нуля?
в) Возрастает или убывает функция при ? при ?
10. Постройте график функции . С помощью графика найдите приближённо:
а) , ;
б) значение , при котором ; .
1. График:
a) Температура была в 2 ч и в 10 ч.
б) Температура возрастала с 6 ч до 14 ч; убывала – с 0 ч до 6 ч и с 16 ч до 24 ч; была положительной – с 0 ч до 2 ч и с 10 ч до 24 ч; была отрицательной – с 2 ч до 10 ч.
в) Максимальное значение температуры ; минимальное значение температуры .
г) Температура в течение суток менялась с до .
д) В 17 ч температура была .
е) Температура была в 13 ч и в 17 ч 20 мин.
;
a) при , ;
при , .
б) при ;
при .
;
a) ;
.
б) ;
.
;
.
;
при ;
, – нули функции.
5. a) , при – нули функции.
б) функция положительна при .
в) функция убывает при .
г) .
6. a) .
б) Через 1 ч после начала движения автобусу останется проехать км; через 2 ч – км; через 4 ч – прибудет во Ржев.
в) В км от Ржева автобус будет находиться через:
ч мин.
В км от Ржева автобус будет находиться через:
ч мин.
г) Графиком данной функции является прямая.
д) Функция является убывающей, так как или расстояние между городами с каждым часом уменьшается.
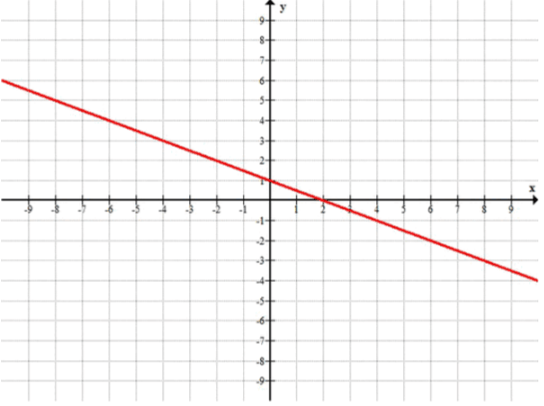
е) График:
7. a) ;
б)
в) ;
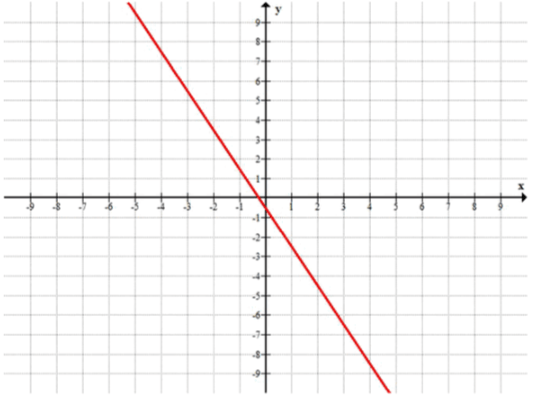
a)
б) Функция убывающая.
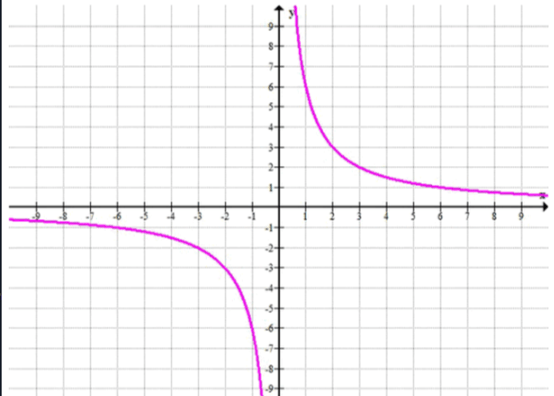
a) Область определения функции:
б)
в) При
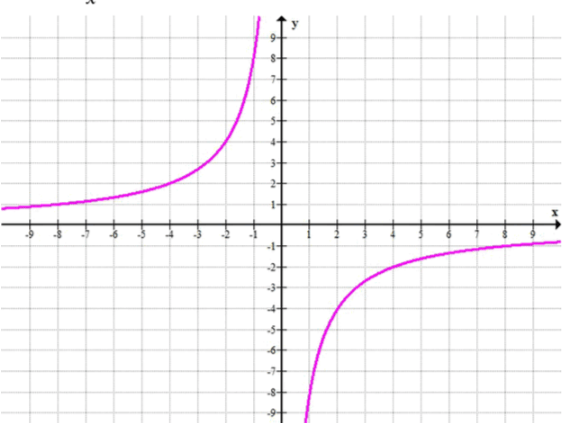
a)
б)
1. График:
a) Температура была
В данном задании говорится о температуре, которая равна
б) Температура возрастала с 6 ч до 14 ч; убывала – с 0 ч до 6 ч и с 16 ч до 24 ч; была положительной – с 0 ч до 2 ч и с 10 ч до 24 ч; была отрицательной – с 2 ч до 10 ч.
Температура возрастала с 6 ч до 14 ч, это значит, что на графике функция будет восходящей на этом интервале времени.
Температура убывала с 0 ч до 6 ч и с 16 ч до 24 ч, что означает нисходящий участок графика на этих интервалах времени.
Температура была положительной с 0 ч до 2 ч и с 10 ч до 24 ч, то есть в этих интервалах график будет находиться выше оси
Температура была отрицательной с 2 ч до 10 ч, то есть в этом интервале график будет ниже оси
в) Максимальное значение температуры
Максимальная температура на графике достигает
г) Температура в течение суток менялась с
График температуры меняется в пределах от
д) В 17 ч температура была
Это просто факт, который показывает, что в момент времени 17 ч температура была
е) Температура была
Температура была
a) при
при
Для того чтобы найти
При
При
б) при
при
Чтобы найти значения
Ответ:
a)
Для нахождения значений функции при различных
При
При
б)
Чтобы найти
Аналогично для
при
Чтобы найти нули функции, решим уравнение
Из этого уравнения получаем два значения для
Ответ: нули функции
5. a)
Это уравнение уже имеет решение:
б) функция положительна при
Функция положительна на интервале
в) функция убывает при
Функция убывает на интервале
г)
Это просто факт, что максимальное значение функции на графике равно
6. a)
Это линейная функция, где
б) Через 1 ч после начала движения автобусу останется проехать
Это задача на нахождение оставшегося расстояния после некоторого времени. Если автобус начинает с 240 км, то для каждого часа его путь сокращается на 60 км.
в) В
Чтобы найти, через сколько часов автобус будет в
г) Графиком данной функции является прямая.
График функции
д) Функция является убывающей, так как
Это указывает на то, что автобус сокращает расстояние с каждым часом, и функция убывает.
7. a)
б)
в)
a)
б) Функция убывающая.
a
a) Область определения функции:
Область определения функции
б)
Теперь рассмотрим знак функции на разных интервалах.
Когда
Когда
в) При
Для того чтобы понять, как функция ведет себя на интервалах
Так как
a)
Для того чтобы найти значения функции при
При
При округлении до одной десятой, получаем:
При
При округлении до одной десятой, получаем:
б)
Чтобы найти значение
Умножим обе части на
Разделим обе части на 5:
Для того чтобы найти значение
Умножим обе части на
Разделим обе части на -7:
Алгебра