Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 837 Дорофеев, Суворова — Подробные Ответы
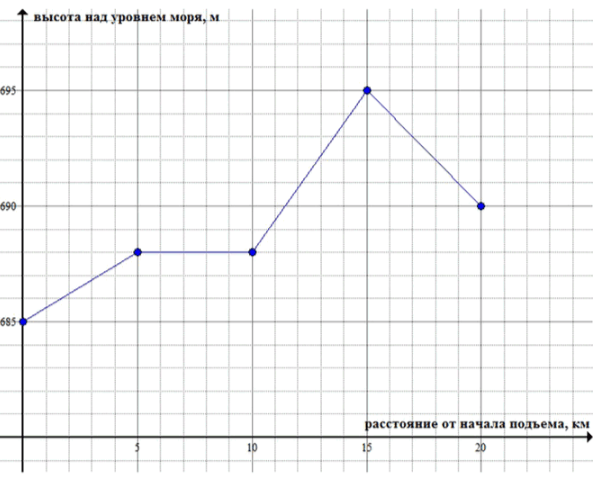
На шоссе, ведущем в гору, через каждые 5 км установлен знак с отметкой высоты над уровнем моря. В таблице приведены данные на первые 20 км этой дороги.
а) Отметьте указанные точки в координатной плоскости.
б) Укажите промежутки, на которых высота растет; не изменяется; снижается.
в) На каком участке шоссе высота над уровнем моря увеличивается с наибольшей скоростью Какова средняя скорость ее увеличения на этом участке (число метров на каждый километр пути)
а) Отметим точки:
;
;
;
;
.
б) Высота растет на промежутках: ; ;
высота не изменяется: ;
высота снижается: .
в) Высота над уровнем моря увеличивается с наибольшей скоростью на участке с до км. Средняя скорость увеличения:
а) Отметим точки:
Задача состоит в том, чтобы рассчитать высоты на разных точках пути. Для этого можно использовать таблицу, которая показывает высоту на разных отметках пути, указанных в этих точках. Каждая точка представляет собой пару чисел, где первое значение — это расстояние вдоль маршрута, а второе — это высота на этом участке.
В точке , высота .
В точке , высота .
В точке , высота .
В точке , высота .
В точке , высота .
Ответ: точки, отмеченные на графике, показывают различные значения высоты на пути.
б) Высота растет на промежутках: ; ;
высота не изменяется: ;
высота снижается: .
Теперь мы анализируем поведение высоты на разных промежутках пути. Для этого:
На промежутке , высота увеличивается от до , следовательно, высота растет.
На промежутке , высота остаётся постоянной, равной , следовательно, высота не изменяется.
На промежутке , высота увеличивается от до , следовательно, высота растет.
На промежутке , высота снижается от до , следовательно, высота снижается.
Ответ: высота растет на промежутках и , не изменяется на , и снижается на .
в) Высота над уровнем моря увеличивается с наибольшей скоростью на участке с до км. Средняя скорость увеличения:
Средняя скорость изменения высоты на промежутке вычисляется по формуле для средней скорости, которая выглядит так:
где — изменение высоты, а — изменение пути.
Для промежутка :
- метров (изменение высоты),
- км (изменение расстояния).
Подставляем в формулу:
Ответ: Средняя скорость увеличения высоты на промежутке от до км составляет .
Алгебра