Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 817 Дорофеев, Суворова — Подробные Ответы
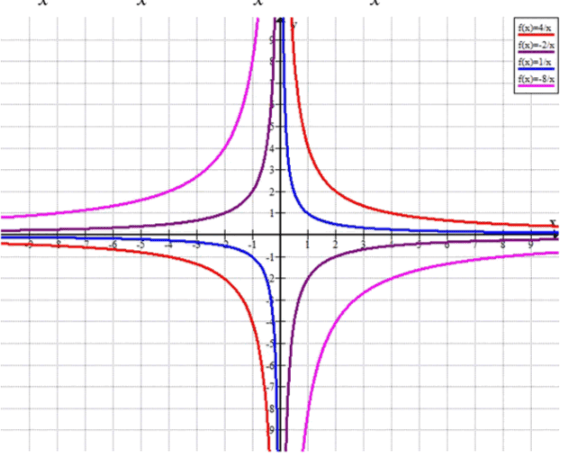
В одной системе координат постройте графики функций:
y=1/x, y=4/x, y=-2/x, y=-8/x. Как зависит расположение графика функции y=k/x от модуля коэффициента k
,
,
,
;
При — функция расположена во второй и четвертой координатных четвертях;
при — в первой и третьей координатных четвертях.
Чем меньше , тем ближе к осям координат расположен график.
,
,
,
;
Эти уравнения представляют собой семейство гипербол, каждая из которых является функцией вида , где — это коэффициент, определяющий «размер» гиперболы. Все эти функции являются обратными пропорциями, так как значение меняется обратно пропорционально . Все эти гиперболы имеют горизонтальную асимптоту и вертикальную асимптоту . Однако различие между ними заключается в величине и знаке коэффициента .
: Здесь . Эта гипербола расположена в первой и третьей координатных четвертях.
: Здесь , что делает гиперболу более «приподнятой» по сравнению с , но она будет иметь тот же вид, только более растянутую.
: Здесь . Этот коэффициент определяет, что график будет перевернут относительно оси и будет расположен в другой части координатной плоскости.
: Здесь . В этом случае гипербола будет более растянутой по сравнению с .
При — функция расположена во второй и четвертой координатных четвертях;
при — в первой и третьей координатных четвертях.
Значение коэффициента влияет на расположение гиперболы в координатной плоскости. При , функция будет располагаться в первой (где и ) и третьей (где и ) координатных четвертях. При , функция будет располагаться во второй (где и ) и четвертой (где и ) координатных четвертях.
Это объясняется тем, что:
Когда , числитель и знаменатель имеют одинаковые знаки на положительных значениях и отрицательные знаки на отрицательных значениях , что делает функцию положительной на и отрицательной на .
Когда , числитель и знаменатель будут иметь противоположные знаки, что приводит к положительному значению функции на и отрицательному значению функции на .
Чем меньше , тем ближе к осям координат расположен график.
Величина оказывает влияние на «сжатие» или «растяжение» графика гиперболы. Когда становится меньшим, то гипербола становится более сжато расположенной, а ее график будет ближе к осям. Например, при , график будет более растянутым, а при , график будет более сжатым, и гипербола будет располагаться ближе к осям.
Когда увеличивается, гипербола будет «расширяться», отдаляясь от осей. Таким образом, для графиков, где больше, гипербола будет выглядеть более «широкой», а для меньших значений график будет ближе к осям.
Итак, график будет приближаться к осям координат по мере того как величина становится меньше.
Алгебра