Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 810 Дорофеев, Суворова — Подробные Ответы
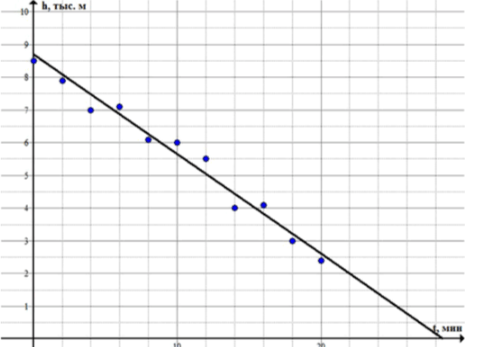
1) Самолет начал снижение на высоте 8500 м. На графике (рис.5.47) показано изменение его высоты над землей в первые 20 мин снижения. Перечертите график в тетрадь и подберите прямую, вокруг которой укладываются эти точки. Определите, сколько примерно минут длилось снижение самолета и какова была средняя скорость снижения (в м/мин).
Снижение самолета длилось примерно мин.
Пусть время снижения самолета составляет минут, где – это время, которое понадобилось для того, чтобы самолет снизился на заданную высоту. Время измеряется в минутах, и это значение нам необходимо для вычисления средней скорости. Средняя скорость описывает, как быстро происходило снижение за весь период.
Средняя скорость снижения самолета:
где:
- — средняя скорость снижения,
- м — общая высота, на которую самолет снизился, измеренная в метрах,
- мин — время снижения.
Нам нужно перевести время в единицы, соответствующие метрам в минуту. Однако для упрощения можно оставить время в минутах, так как результат будет получен в метрах на минуту.
Подставляем известные значения:
Таким образом, средняя скорость снижения самолета составляет примерно метра в минуту.
Алгебра