ГДЗ по Алгебре 8 Класс Номер 805 Дорофеев, Суворова — Подробные Ответы

Скорость звука в воздухе примерно 0,3 км/с. Во время грозы вы сначала видите молнию и льши через некоторое время слышите гром. Задайте формулой функцию y=f(x), где:
а) y — расстояние, на котором вы находитесь от места удара молнии, x — время между вспышкой молнии и громом;
б) y — время между вспышкой молнии и громом, x — расстояние, на котором вы находитесь от места удара молнии. Постройте график каждой функции.

а) $y = 0.3x$;

б) $y = \frac{x}{0.3}$;

Для того чтобы дать максимально подробное решение, давайте разберем каждую функцию и ее особенности по шагам, начиная с анализа данных и заканчивая выводами.

Шаг 1: Анализ функции $y = 0.3x$

Это линейная функция, которая имеет вид $y = mx$, где $m = 0.3$ — коэффициент наклона. В этой функции нет постоянного слагаемого, что означает, что график будет проходить через начало координат (точку $(0, 0)$).

Наклон прямой:
Коэффициент $0.3$ указывает на то, что для каждого увеличения $x$ на 1, значение $y$ увеличивается на 0.3. Это означает, что функция возрастает с постоянной скоростью, то есть график будет прямой, а наклон будет положительным, что указывает на возрастающий характер функции.

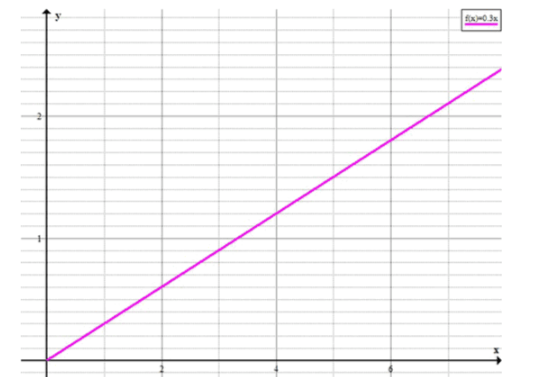
График:
График этой функции будет прямой линией, которая проходит через начало координат $(0, 0)$ и имеет наклон, равный 0.3. Он будет подниматься вверх по мере увеличения значения $x$.

Пример вычислений для различных значений $x$:

• При $x = 1$, подставляем в уравнение:

$$y = 0.3 \cdot 1 = 0.3$$

• При $x = 2$, подставляем в уравнение:

$$y = 0.3 \cdot 2 = 0.6$$

• При $x = -1$, подставляем в уравнение:

$$y = 0.3 \cdot (-1) = -0.3$$

Это подтверждает, что функция возрастает с постоянной скоростью, и значение $y$ увеличивается или уменьшается в зависимости от знака $x$.

Шаг 2: Анализ функции $y = \frac{x}{0.3}$

Это также линейная функция, но с разным коэффициентом наклона. Мы можем преобразовать её в форму $y = mx + b$, где $m = \frac{1}{0.3}$. Посмотрим, как это влияет на график.

Преобразование функции:
Мы можем переписать уравнение следующим образом:

$$y = \frac{x}{0.3} = \frac{10}{3}x$$

Это означает, что коэффициент наклона функции будет равен $\frac{10}{3} \approx 3.33$. Это говорит о том, что график этой функции будет возрастать намного быстрее, чем график функции $y = 0.3x$, так как наклон значительно больше.

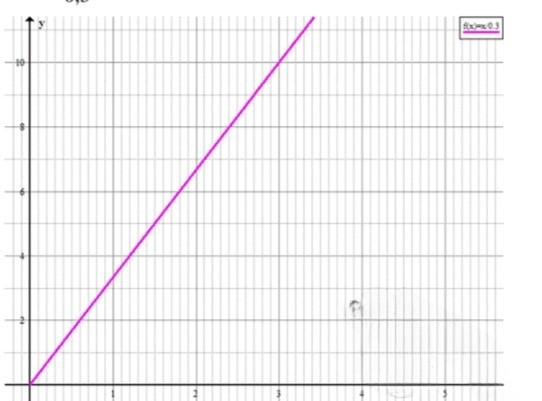
График:
График функции будет также прямой линией, которая проходит через начало координат $(0, 0)$, но с более крутым наклоном. Это объясняется тем, что коэффициент наклона $m = \frac{10}{3}$ значительно больше, чем $0.3$.

Пример вычислений для различных значений $x$:

• При $x = 1$, подставляем в уравнение:

$$y = \frac{1}{0.3} = \frac{10}{3} \approx 3.33$$

• При $x = 2$, подставляем в уравнение:

$$y = \frac{2}{0.3} = \frac{20}{3} \approx 6.67$$

• При $x = -1$, подставляем в уравнение:

$$y = \frac{-1}{0.3} = \frac{-10}{3} \approx -3.33$$

Это подтверждает, что при увеличении $x$, значение $y$ растет с более быстрым темпом по сравнению с функцией $y = 0.3x$.

Шаг 3: Сравнение двух функций

Теперь, когда мы проанализировали обе функции, можно сделать выводы о том, как они ведут себя на графике и как сравниваются между собой.

Графики:

График функции $y = 0.3x$ — это прямая линия с относительно пологим наклоном.

График функции $y = \frac{x}{0.3}$ — это прямая линия с крутым наклоном, которая возрастает намного быстрее.

Преимущества и различия:

Функция $y = 0.3x$ имеет меньший коэффициент наклона, что означает, что она будет увеличиваться медленнее. Это подойдет для случаев, когда необходимо более плавное увеличение величины с течением времени.

• Функция $y = \frac{x}{0.3}$ имеет более крутой наклон, что означает, что она будет увеличиваться гораздо быстрее. Эта функция будет полезна для ситуаций, когда нужно достичь более быстрого роста в зависимости от $x$.

Шаг 4: Выводы

Функция $y = 0.3x$: Это функция с более пологим наклоном, где увеличение значения $y$ происходит медленно с увеличением $x$.

Функция $y = \frac{x}{0.3}$: Эта функция растет быстрее, поскольку наклон у нее круче. Для каждого изменения $x$ изменение $y$ происходит быстрее.

Эти функции хорошо демонстрируют, как изменение коэффициента наклона влияет на скорость изменения значения функции при изменении переменной $x$.