ГДЗ по Алгебре 8 Класс Номер 804 Дорофеев, Суворова — Подробные Ответы

Муравей ползет по шесту для флага, воткнутому вертикально в землю. Длина шеста 4 м. Муравей начал свой путь в 20 см от земли и ползет вверх с посотоянной скоростью 40 см/мин.
а) Задайте формулой расстояние s, на котором находится муравей от земли, как функцию времени его движения t.
б) Укажите область определения этой функции.
в) Постройте график функции, выбрав удобные единицы на осях.
г) Определите по графику, на какой высоте от земли муравей будет через 3 мин и через сколько минут он доползет до вершины шеста.

а) Пусть $s$ — расстояние в см, а $t$ — время в мин;
$s = 40t + 20$.

б) Область определения: $0 \leq t \leq 9.5$;
$40t + 20 \leq 400$
$2t + 1 \leq 20$
$t \leq 9.5$.

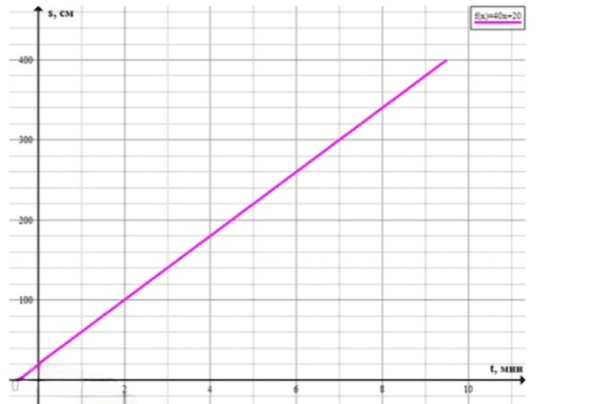
в) График:

г) Через 3 мин муравей будет на высоте $140$ см;
до вершины шеста муравей доползет через $9.5$ мин.

Для подробного решения задачи, давайте сначала разобьем задачу на части и объясним каждый шаг, чтобы более детально понять, как решается эта задача с учетом предоставленных данных.

Шаг 1: Анализ функции

Дана линейная зависимость между расстоянием $s$ и временем $t$:

$$s = 40t + 20$$

Здесь $s$ — это расстояние в сантиметрах, а $t$ — это время в минутах. Мы видим, что эта функция линейная, так как выражение для $s$ имеет вид $y = mx + b$, где $m = 40$ — это коэффициент наклона, а $b = 20$ — это начальное значение на оси $y$, то есть на момент $t = 0$, расстояние $s = 20$ см.

Шаг 2: Определение области определения функции

Область определения функции — это значения $t$, для которых функция имеет смысл, то есть для которых расстояние $s$ будет удовлетворять ограничению, что оно не может превышать максимальное расстояние (например, длина шеста).

Дано, что $40t + 20 \leq 400$. Мы можем решить это неравенство:

$$40t + 20 \leq 400$$

Вычитаем 20 из обеих сторон:

$$40t \leq 380$$

Теперь делим обе стороны на 40:

$$t \leq \frac{380}{40} = 9.5$$

Таким образом, $t \leq 9.5$. Значит, область определения функции: $0 \leq t \leq 9.5$. Это означает, что время $t$ не может быть меньше 0 и не может превышать 9.5 минут, так как это максимальное время, за которое муравей доберется до вершины шеста.

Шаг 3: Понимание графика

График функции будет прямой линией, так как у нас линейная зависимость. Наклон этой линии будет равен 40 (это скорость муравья, 40 см/мин), а точка пересечения с осью $y$ (начальная точка) будет на высоте 20 см.

График будет начинаться от точки $(0, 20)$, что означает, что в момент времени $t = 0$, муравей уже находится на высоте 20 см от земли. С увеличением времени $t$, высота будет увеличиваться с постоянной скоростью, равной 40 см/мин.

Шаг 4: Определение высоты через 3 минуты

Для того чтобы найти высоту муравья через 3 минуты, подставим $t = 3$ в уравнение:

$$s = 40 \cdot 3 + 20 = 120 + 20 = 140 \, \text{см}$$

Таким образом, через 3 минуты муравей будет находиться на высоте 140 см.

Шаг 5: Определение времени для достижения вершины

Теперь, чтобы узнать, через сколько минут муравей доберется до вершины шеста (400 см), подставим $s = 400$ в уравнение:

$$400 = 40t + 20$$

Вычитаем 20 из обеих сторон:

$$380 = 40t$$

Делим обе стороны на 40:

$$t = \frac{380}{40} = 9.5 \, \text{минут}$$

Таким образом, для того чтобы муравей добрался до вершины шеста, ему потребуется 9.5 минут.