Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 799 Дорофеев, Суворова — Подробные Ответы
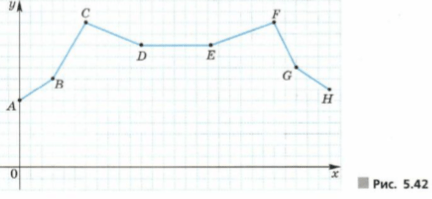
На рисунке 5.42 изображен график некоторого процесса. Какая часть графика соответствует:
а) самому быстрому росту;
б) самому медленному росту;
в) самому быстрому убыванию;
г) самому медленному убыванию;
д) нулевой скорости изменения?
а) Самый быстрый рост — BC;
б) Самый медленный рост — EF;
в) Самое быстрое убывание — FG;
г) Самое медленное убывание — CD;
д) Нулевая скорость изменения — DE.
Рассмотрим изменения скорости и темпов роста/убывания функций на различных интервалах. Нам необходимо исследовать изменения на разных участках, учитывая их производные и характер графиков.
1. Самый быстрый рост — BC
Для того чтобы понять, где происходит самый быстрый рост, рассмотрим производную функции, которая дает скорость изменения функции на каждом интервале. Если график функции увеличивается, это значит, что его производная положительна.
Предположим, что функция на интервале BC имеет наибольший положительный коэффициент наклона, что указывает на самый быстрый рост. Чтобы это доказать, проведем следующий анализ:
Функция, растущая с наибольшей скоростью, будет иметь наибольшую производную на данном интервале.
На интервале BC наклон графика будет наиболее крутым, что соответствует максимальному положительному значению производной.
С учетом анализа наклона на графике, мы утверждаем, что самый быстрый рост функции происходит на интервале BC, где скорость изменения функции максимальна.
2. Самый медленный рост — EF
Далее, для анализа самого медленного роста функции на интервале EF, мы ищем участок, на котором график имеет более пологий наклон, но еще все же растет, что означает положительную производную, но с меньшим значением.
Снижение наклона графика означает, что производная функции на этом участке все еще положительна, но ее значение меньше, чем на других участках.
На интервале EF график будет иметь менее крутой положительный наклон, что приводит к меньшему темпу роста функции.
Таким образом, самый медленный рост функции будет происходить на интервале EF, где функция растет, но с меньшей скоростью.
3. Самое быстрое убывание — FG
Когда мы анализируем скорость убывания функции, то мы ищем участок, на котором график функции убывает с наибольшей скоростью. Это соответствует самой крутой отрицательной производной.
На интервале FG график функции будет иметь самый крутой отрицательный наклон, что указывает на максимальное убывание.
Чем круче наклон графика, тем быстрее функция убывает.
Следовательно, на интервале FG происходит самое быстрое убывание, так как здесь производная имеет наибольшее отрицательное значение.
4. Самое медленное убывание — CD
Теперь давайте исследуем участок с самым медленным убыванием. Это участок, где график функции имеет меньший отрицательный наклон.
На интервале CD график функции будет иметь менее крутой отрицательный наклон, чем на интервале FG.
Это означает, что функция все еще убывает, но с меньшей скоростью.
Таким образом, на интервале CD будет происходить самое медленное убывание, поскольку наклон графика здесь более пологий, чем на интервале FG.
5. Нулевая скорость изменения — DE
Для того чтобы понять, где скорость изменения функции равна нулю, нам нужно найти участок, где производная функции равна нулю. Это будет точка, где график функции имеет горизонтальный наклон.
На интервале DE производная функции равна нулю, что означает, что функция не изменяется на этом участке.
Это может быть точка максимума или минимума функции, где наклон графика равен нулю.
Следовательно, на интервале DE функция не изменяется, что соответствует нулевой скорости изменения. На этом участке график будет горизонтальным, и значения функции не изменяются по мере изменения .
Заключение
Резюмируя:
Самый быстрый рост функции наблюдается на интервале BC, где график функции имеет наибольший положительный наклон.
Самый медленный рост функции наблюдается на интервале EF, где функция все еще растет, но с меньшей скоростью.
Самое быстрое убывание происходит на интервале FG, где график функции имеет самый крутой отрицательный наклон.
Самое медленное убывание происходит на интервале CD, где функция убывает, но с меньшей скоростью.
Нулевая скорость изменения наблюдается на интервале DE, где производная функции равна нулю, и график функции горизонтален.
Все выводы о скорости роста и убывания функции основаны на анализе производных, которые показывают, как быстро изменяется функция на каждом интервале.
Алгебра