ГДЗ по Алгебре 8 Класс Номер 798 Дорофеев, Суворова — Подробные Ответы

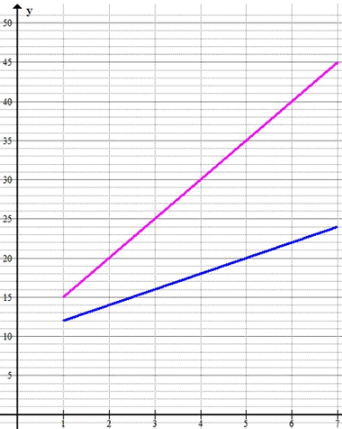
а) У вас имеется 10 р. и есть два способа увеличить эту сумму: ежедневно добавлять к ней 5 р. или ежедневно добавлять к ней 2 р. Составьте для каждого случая формулу зависимости имеющейся суммы денег y от числа дней x. В каком случае сумма будет увеличиваться быстрее? В одной системе координат постройте прямые, которым принадлежат точки графика каждой из функций, и отметьте эти точки для 1 < =x < =7.
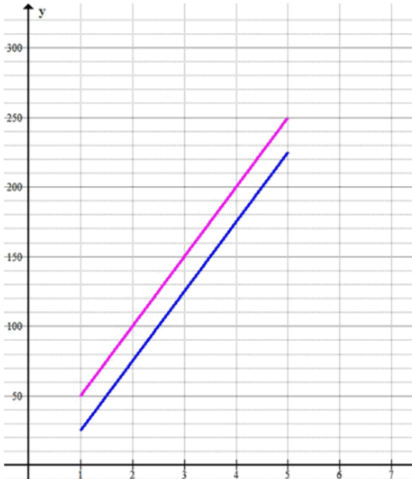
б) Андрей планирует поработать во время летних каникул, и у него есть две возможности. На работе A он будет получать 50 р. в день. На работе B он в первый день получит 25 р., а затем ежедневно будет получать 50 р. Какой вариант выгоднее? Составьте формулу зависимости полученной суммы денег y от числа рабочих дней x для вариантов A и B. В одной системе координат постройте прямые, которым принадлежат точки графика каждой из функций, и отметьте эти точки для 1 < =x < =5. Существуют ли значения x, при которых значения y равны?

а) $y = 10 + 5x$; $y = 10 + 2x$;
В первом случае сумма будет увеличиваться быстрее.
$1 \leq x \leq 7$;

б) $y = 50x$; $y = 50x — 25$;
Выгоднее вариант А.
$1 \leq x \leq 5$.
Значений $x$ не существует, при которых значения $y$ равны, так как прямые параллельны.

Для решения задачи, рассмотрим сначала первую часть — функции, описанные в пункте а):

$y = 10 + 5x$ и $y = 10 + 2x$.

Анализ функций:

Мы имеем две линейные функции, где:

Функция $y = 10 + 5x$ имеет коэффициент при $x$ равный $5$, что указывает на более быстрый рост значения функции по сравнению с функцией $y = 10 + 2x$, где коэффициент при $x$ равен $2$.

Сравнение роста:

Чтобы понять, как быстро растет каждая функция, обратим внимание на коэффициенты при $x$. Для функции $y = 10 + 5x$, рост значения функции на 1 единицу $x$ равен 5, в то время как для функции $y = 10 + 2x$, рост на 1 единицу $x$ равен 2. Это означает, что с увеличением $x$, сумма для функции $y = 10 + 5x$ будет увеличиваться быстрее, чем для функции $y = 10 + 2x$.

Решение для интервала $1 \leq x \leq 7$:

При $x = 1$, для функции $y = 10 + 5x$, получаем:

$$y = 10 + 5 \cdot 1 = 15$$

При $x = 1$, для функции $y = 10 + 2x$, получаем:

$$y = 10 + 2 \cdot 1 = 12$$

При $x = 7$, для функции $y = 10 + 5x$, получаем:

$$y = 10 + 5 \cdot 7 = 45$$

При $x = 7$, для функции $y = 10 + 2x$, получаем:

$$y = 10 + 2 \cdot 7 = 24$$

Таким образом, на интервале от $x = 1$ до $x = 7$, функция $y = 10 + 5x$ дает значения, которые увеличиваются быстрее, чем функция $y = 10 + 2x$, так как при одинаковых значениях $x$ для второй функции результат всегда будет меньше.

Теперь переходим ко второй части — рассмотрим функции, описанные в пункте б):

$y = 50x$ и $y = 50x — 25$.

Анализ функций:

Обе функции имеют одинаковый коэффициент при $x$, равный $50$, что означает, что они растут с одинаковой скоростью. Однако, вторая функция $y = 50x — 25$ отличается от первой тем, что имеет сдвиг по оси $y$ на $-25$, то есть, её график будет смещён вниз на 25 единиц по сравнению с первой функцией.

Поиск пересечения:

Теперь давайте найдем, при каких значениях $x$ функции $y = 50x$ и $y = 50x — 25$ могут быть равны. Для этого приравняем их:

$$50x = 50x — 25$$

Теперь вычитаем $50x$ с обеих сторон:

$$0 = -25$$

Это невозможно. Это означает, что этих функций нет общих решений, то есть, их графики никогда не пересекаются, и прямые являются параллельными.

Заключение для второй части:

• В функции $y = 50x$ и $y = 50x — 25$ нет значений $x$, при которых значения $y$ равны, потому что прямые параллельны.
• В этом случае, на интервале $1 \leq x \leq 5$, значение $y$ будет одинаково расти для обеих функций, но сдвиг по оси $y$ у второй функции будет постоянным, то есть она будет всегда ниже первой на 25 единиц.
• В итоге, из двух вариантов, более выгодным является первый вариант $y = 50x$, так как там значения функции для каждого $x$ больше, чем в варианте $y = 50x — 25$.