ГДЗ по Алгебре 8 Класс Номер 797 Дорофеев, Суворова — Подробные Ответы

В одной системе координат постройте графики линейных функций y=f(x) и y=g(x) и определите значения x, при которых f(x)=g(x); f(x) > g(x); f(x) < g(x):
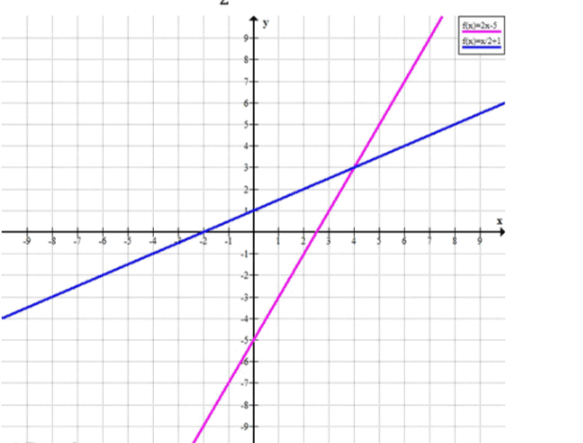
а) f(x)=2x-5; g(x)=1/2 x+1;
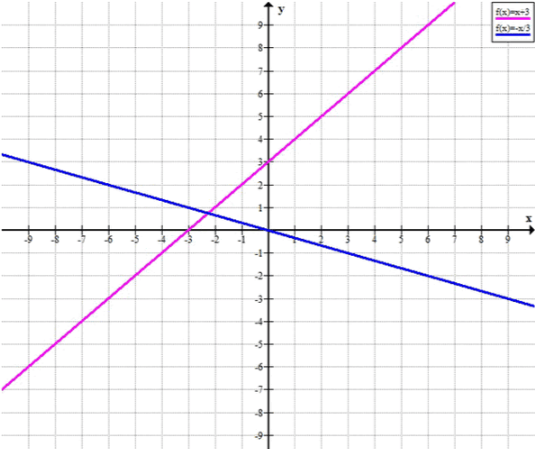
б) f(x)=x+3; g(x)=-1/3 x.

а) $f(x) = 2x — 5$; $g(x) = \frac{1}{2}x + 1$;
$f(x) = g(x)$, при $x = 4$;
$f(x) > g(x)$, при $x > 4$;
$f(x) < g(x)$, при $x < 4$.

б) $f(x) = x + 3$; $g(x) = -\frac{1}{3}x$;
$f(x) = g(x)$;
$x + 3 = -\frac{1}{3}x$
$x + \frac{1}{3}x = -3$
$\frac{4}{3}x = -3$
$x = -3 \cdot \frac{3}{4} = -2.25$.
$f(x) > g(x)$, при $x > -2.25$;
$f(x) < g(x)$, при $x < -2.25$.

Для функции $f(x) = 2x — 5$ и $g(x) = \frac{1}{2}x + 1$ давайте рассмотрим их пересечение, а также то, как изменяются значения этих функций относительно друг друга на разных интервалах.

1. Равенство функций $f(x) = g(x)$

Чтобы найти точку пересечения графиков этих функций, приравняем их:

$$f(x) = g(x)$$

Подставим выражения для $f(x)$ и $g(x)$:

$$2x — 5 = \frac{1}{2}x + 1$$

Теперь решим это уравнение. Начнем с того, чтобы избавиться от дробей. Умножим обе части на 2:

$$2 \cdot (2x — 5) = 2 \cdot \left( \frac{1}{2}x + 1 \right)$$ $$4x — 10 = x + 2$$

Теперь перенесем все элементы с $x$ в одну сторону, а все остальные числа — в другую:

$$4x — x = 2 + 10$$ $$3x = 12$$

Теперь поделим обе части на 3:

$$x = \frac{12}{3} = 4$$

Таким образом, функции $f(x)$ и $g(x)$ равны при $x = 4$. Точка пересечения этих функций — $x = 4$.

2. Определение, где $f(x) > g(x)$ и $f(x) < g(x)$

Чтобы понять, где одна функция больше другой, проведем анализ знаков разности этих функций. Рассмотрим выражение:

$$f(x) — g(x) = \left( 2x — 5 \right) — \left( \frac{1}{2}x + 1 \right)$$

Приводим подобные члены:

$$f(x) — g(x) = 2x — 5 — \frac{1}{2}x — 1$$ $$f(x) — g(x) = \left( 2x — \frac{1}{2}x \right) — 6$$ $$f(x) — g(x) = \frac{3}{2}x — 6$$

Теперь анализируем знак этой разности:

• Если $f(x) — g(x) > 0$, то $f(x) > g(x)$.
• Если $f(x) — g(x) < 0$, то $f(x) < g(x)$.

Решим неравенство $f(x) — g(x) > 0$:

$$\frac{3}{2}x — 6 > 0$$

Добавим 6 к обеим частям:

$$\frac{3}{2}x > 6$$

Теперь умножим обе части на $\frac{2}{3}$:

$$x > 4$$

Следовательно, $f(x) > g(x)$, когда $x > 4$.

Теперь решим неравенство $f(x) — g(x) < 0$:

$$\frac{3}{2}x — 6 < 0$$

Добавим 6 к обеим частям:

$$\frac{3}{2}x < 6$$

Теперь умножим обе части на $\frac{2}{3}$:

$$x < 4$$

Следовательно, $f(x) < g(x)$, когда $x < 4$.

3. Ответ для графика 1

Из анализа следует, что:

• $f(x) = g(x)$ при $x = 4$.
• $f(x) > g(x)$ при $x > 4$.
• $f(x) < g(x)$ при $x < 4$.

Теперь рассмотрим вторую пару функций, $f(x) = x + 3$ и $g(x) = -\frac{1}{3}x$.

1. Равенство функций $f(x) = g(x)$

Для нахождения точки пересечения этих функций приравняем их:

$$f(x) = g(x)$$

Подставим выражения для $f(x)$ и $g(x)$:

$$x + 3 = -\frac{1}{3}x$$

Теперь умножим обе части на 3, чтобы избавиться от дроби:

$$3 \cdot \left( x + 3 \right) = 3 \cdot \left( -\frac{1}{3}x \right)$$ $$3x + 9 = -x$$

Переносим все элементы с $x$ в одну сторону:

$$3x + x = -9$$ $$4x = -9$$

Теперь делим обе части на 4:

$$x = \frac{-9}{4} = -2.25$$

Таким образом, $f(x) = g(x)$ при $x = -2.25$.

2. Определение, где $f(x) > g(x)$ и $f(x) < g(x)$

Теперь рассмотрим разницу между функциями:

$$f(x) — g(x) = \left( x + 3 \right) — \left( -\frac{1}{3}x \right)$$

Приводим подобные члены:

$$f(x) — g(x) = x + 3 + \frac{1}{3}x$$ $$f(x) — g(x) = \frac{3}{3}x + \frac{1}{3}x + 3$$ $$f(x) — g(x) = \frac{4}{3}x + 3$$

Теперь решим неравенства для $f(x) — g(x)$:

Для $f(x) > g(x)$, решаем неравенство:

$$\frac{4}{3}x + 3 > 0$$

Отнимем 3 от обеих частей:

$$\frac{4}{3}x > -3$$

Теперь умножим обе части на $\frac{3}{4}$:

$$x > -2.25$$

Для $f(x) < g(x)$, решаем неравенство:

$$\frac{4}{3}x + 3 < 0$$

Отнимем 3 от обеих частей:

$$\frac{4}{3}x < -3$$

Теперь умножим обе части на $\frac{3}{4}$:

$$x < -2.25$$

3. Ответ для графика 2

Таким образом:

• $f(x) = g(x)$ при $x = -2.25$.
• $f(x) > g(x)$ при $x > -2.25$.
• $f(x) < g(x)$ при $x < -2.25$.

Теперь для функции $y = -0.7x$.

Функция убывает, так как коэффициент $-0.7$ отрицателен.

$f(x) = 0$ при $x = 0$.

$f(x) > 0$ при $x < 0$.

$f(x) < 0$ при $x > 0$.

Ответ:

Функция убывает.

$f(x) = 0$ при $x = 0$.

$f(x) > 0$ при $x < 0$.

$f(x) < 0$ при $x > 0$.

Таким образом, все шаги и объяснения приведены.