ГДЗ по Алгебре 8 Класс Номер 794 Дорофеев, Суворова — Подробные Ответы

Постройте график линейной функции. В каждом случае укажите:
1) возрастающей или убывающей является функция;
2) при каких значениях x значения функции равны 0; больше 0; меньше 0.
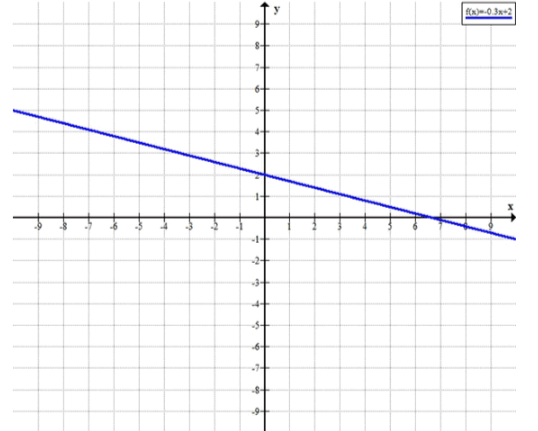
а) y=-0,3x+2;
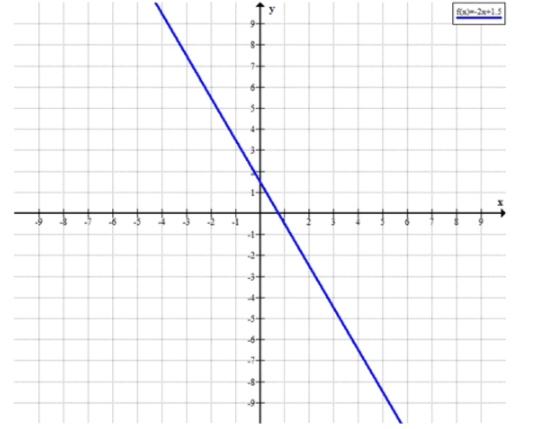
б) y=-2x+1,5;
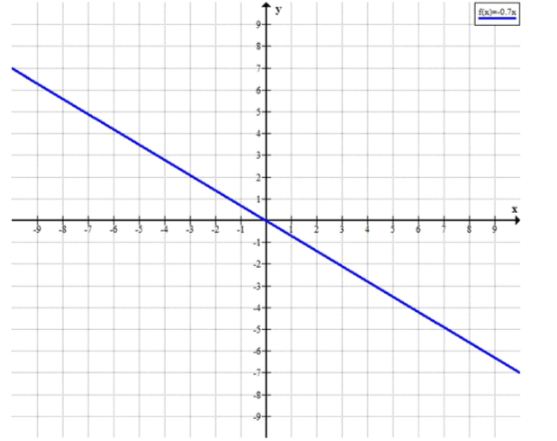
в) y=-0,7x;
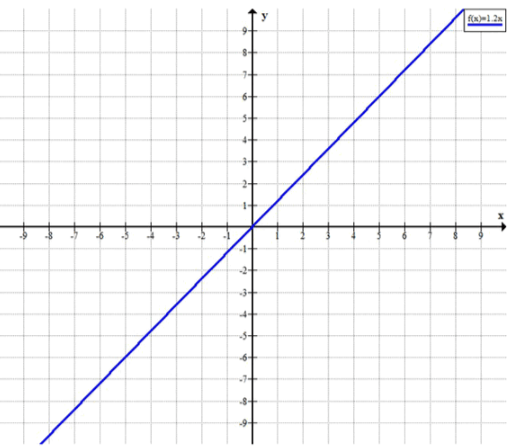
г) y=1,2x;
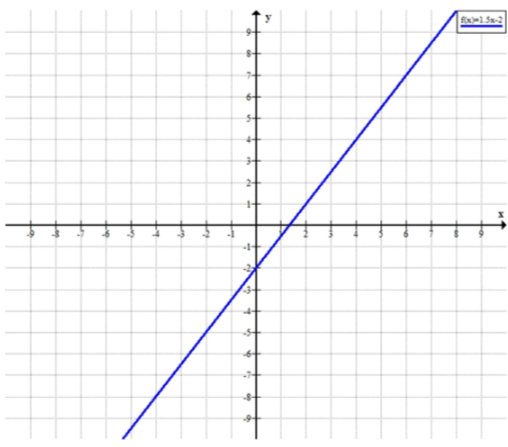
д) y=1,5x-2;
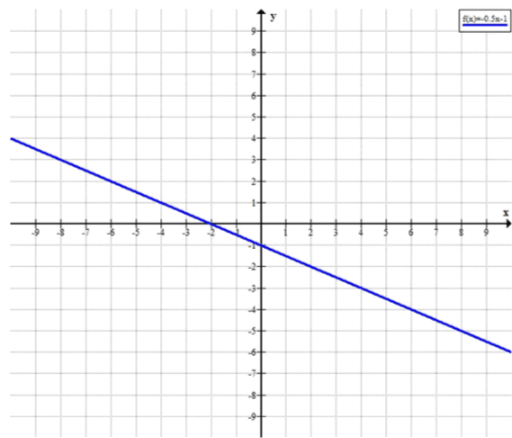
е) y=-0,5x-1.

а) $y = -0.3x + 2$;

убывающая функция;

$y = 0$;
$-0.3x + 2 = 0$,
$0.3x = 2$,
$x = \frac{20}{3}$;
$y > 0$ при $x < \frac{20}{3}$;
$y < 0$ при $x > \frac{20}{3}$.

б) $y = -2x + 1.5$;

убывающая функция;

$y = 0$;
$-2x + 1.5 = 0$,
$2x = 1.5$,
$x = 0.75$;
$y > 0$ при $x < 0.75$;
$y < 0$ при $x > 0.75$.

в) $y = -0.7x$;

убывающая функция;

$y = 0$ при $x = 0$;
$y > 0$ при $x < 0$;
$y < 0$ при $x > 0$.

г) $y = 1.2x$;

возрастающая функция;

$y = 0$ при $x = 0$;
$y > 0$ при $x > 0$;
$y < 0$ при $x < 0$.

д) $y = 1.5x — 2$;

возрастающая функция;

$y = 0$;
$1.5x — 2 = 0$,
$1.5x = 2$,
$x = \frac{2}{1.5} = \frac{4}{3}$;
$y > 0$ при $x > \frac{4}{3}$;
$y < 0$ при $x < \frac{4}{3}$.

е) $y = -0.5x — 1$;

1. убывающая функция;
2. $y = 0$, при $x = -2$;
   $y > 0$, при $x < -2$;
   $y < 0$, при $x > -2$.

а) Рассмотрим функцию $y = -0.3x + 2$. Эта функция представляет собой линейную зависимость, где коэффициент при $x$ равен $-0.3$, а свободный член $2$ указывает на значение функции при $x = 0$.

Монотонность функции
Функция линейная с коэффициентом при $x$, равным $k = -0.3$, что означает, что функция убывает. Это связано с тем, что коэффициент перед $x$ отрицателен, и для каждого увеличения $x$ на 1, значение функции будет уменьшаться на 0.3.

Нахождение корня функции
Для нахождения корня функции, когда $y = 0$, решим уравнение:

$$-0.3x + 2 = 0$$

Приводим уравнение к следующему виду:

$$-0.3x = -2$$

Делим обе части на $-0.3$:

$$x = \frac{-2}{-0.3} = \frac{20}{3}$$

Таким образом, функция пересекает ось $x$ в точке $\left( \frac{20}{3}; 0 \right)$.

Знак функции на разных интервалах
Поскольку функция убывает, она будет иметь положительное значение, когда $x$ меньше $\frac{20}{3}$, и отрицательное значение, когда $x$ больше $\frac{20}{3}$. Следовательно:

$y > 0$ при $x < \frac{20}{3}$

$y < 0$ при $x > \frac{20}{3}$

Ответ:

Функция убывает.

$f(x) = 0$ при $x = \frac{20}{3}$.

$y > 0$ при $x < \frac{20}{3}$; $y < 0$ при $x > \frac{20}{3}$.

б) Рассмотрим функцию $y = -2x + 1.5$. Эта функция также линейная, но с коэффициентом $k = -2$, который указывает на более крутой спад функции по сравнению с функцией в пункте (а).

Монотонность функции
Коэффициент $k = -2$ указывает на то, что функция убывает, и с каждым увеличением $x \ на 1$, значение функции будет уменьшаться на 2.

Нахождение корня функции
Для нахождения корня функции, когда $y = 0$, решим уравнение:

$$-2x + 1.5 = 0$$

Приводим уравнение к следующему виду:

$$-2x = -1.5$$

Делим обе части на $-2$:

$$x = \frac{-1.5}{-2} = 0.75$$

Таким образом, функция пересекает ось $x$ в точке $(0.75; 0)$.

Знак функции на разных интервалах
Поскольку функция убывает, она будет иметь положительное значение, когда $x$ меньше 0.75, и отрицательное значение, когда $x$ больше 0.75. Следовательно:

$y > 0$ при $x < 0.75$

$y < 0$ при $x > 0.75$

Ответ:

Функция убывает.

$f(x) = 0$ при $x = 0.75$.

$y > 0$ при $x < 0.75$; $y < 0$ при $x > 0.75$.

в) Рассмотрим функцию $y = -0.7x$. Эта функция линейная, и с коэффициентом $k = -0.7$, который указывает на убывание функции.

Монотонность функции
Поскольку коэффициент $k = -0.7$ отрицателен, это означает, что функция убывает. Для каждого увеличения $x$ на 1, значение функции будет уменьшаться на 0.7.

Нахождение корня функции
Для нахождения корня функции, когда $y = 0$, решим уравнение:

$$-0.7x = 0$$

Решаем уравнение:

$$x = 0$$

Таким образом, функция пересекает ось $x$ в точке $(0; 0)$.

Знак функции на разных интервалах
Функция убывает, следовательно:

$y > 0$ при $x < 0$

$y < 0$ при $x > 0$

Ответ:

Функция убывает.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x < 0$; $y < 0$ при $x > 0$.

г) Рассмотрим функцию $y = 1.2x$. Эта функция линейная с коэффициентом $k = 1.2$, который положителен, значит, функция возрастает.

Монотонность функции
Поскольку коэффициент $k = 1.2$ положителен, функция возрастает. Это означает, что с каждым увеличением $x$ значение функции будет увеличиваться.

Нахождение корня функции
Для нахождения корня функции, когда $y = 0$, решим уравнение:

$$1.2x = 0$$

Решаем уравнение:

$$x = 0$$

Таким образом, функция пересекает ось $x$ в точке $(0; 0)$.

Знак функции на разных интервалах
Поскольку функция возрастает, она будет иметь положительное значение для всех $x > 0$ и отрицательное значение для всех $x < 0$. Следовательно:

$y > 0$ при $x > 0$

$y < 0$ при $x < 0$

Ответ:

Функция возрастает.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x > 0$; $y < 0$ при $x < 0$.

д) Рассмотрим функцию $y = 1.5x — 2$. Эта функция также линейная с коэффициентом $k = 1.5$, который положителен, и свободным членом $-2$.

Монотонность функции
Поскольку коэффициент $k = 1.5$ положителен, функция возрастает. Это означает, что с увеличением $x$ значение функции будет увеличиваться.

Нахождение корня функции
Для нахождения корня функции, когда $y = 0$, решим уравнение:

$$1.5x — 2 = 0$$

Решаем уравнение:

$$1.5x = 2$$ $$x = \frac{2}{1.5} = \frac{4}{3}$$

Таким образом, функция пересекает ось $x$ в точке $\left( \frac{4}{3}; 0 \right)$.

Знак функции на разных интервалах
Поскольку функция возрастает, она будет иметь положительное значение для всех $x > \frac{4}{3}$ и отрицательное значение для всех $x < \frac{4}{3}$. Следовательно:

$y > 0$ при $x > \frac{4}{3}$

$y < 0$ при $x < \frac{4}{3}$

Ответ:

Функция возрастает.

$f(x) = 0$ при $x = \frac{4}{3}$.

$y > 0$ при $x > \frac{4}{3}$; $y < 0$ при $x < \frac{4}{3}$.

е) Рассмотрим функцию $y = -0.5x — 1$. Эта функция линейная с коэффициентом $k = -0.5$, что означает, что она убывает.

Монотонность функции
Поскольку коэффициент $k = -0.5$ отрицателен, функция убывает. С каждым увеличением $x$ на 1, значение функции будет уменьшаться на 0.5.

Нахождение корня функции
Для нахождения корня функции, когда $y = 0$, решим уравнение:

$$-0.5x — 1 = 0$$

Решаем уравнение:

$$-0.5x = 1$$ $$x = \frac{-1}{0.5} = -2$$

Таким образом, функция пересекает ось $x$ в точке $(-2; 0)$.

Знак функции на разных интервалах
Поскольку функция убывает, она будет иметь положительное значение для всех $x < -2$ и отрицательное значение для всех $x > -2$. Следовательно:

$y > 0$ при $x < -2$

$y < 0$ при $x > -2$

Ответ:

Функция убывает.

$f(x) = 0$ при $x = -2$.

$y > 0$ при $x < -2$; $y < 0$ при $x > -2$.