ГДЗ по Алгебре 8 Класс Номер 783 Дорофеев, Суворова — Подробные Ответы

Постройте график функции и прочитайте по графику ее свойства:
а) y=x^2; б) y=-x^3; в) y=|x|; г) y=vx.

а) $y = x^2$;

$y_{\text{наиб}}$ — не существует; $y_{\text{наим}} = 0$.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (-\infty; 0)$ и $x \in (0; +\infty)$;
$y < 0$ — нет.

функция возрастает на $[0; +\infty)$,
функция убывает на $(-\infty; 0]$.

б) $y = -x^3$;

$y_{\text{наиб}}$ и $y_{\text{наим}}$ — не существуют.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (-\infty; 0)$;
$y < 0$ при $x \in (0; +\infty)$.

функция убывает на $(-\infty; +\infty)$.

в) $y = |x|$;

$y_{\text{наиб}}$ — не существует; $y_{\text{наим}} = 0$.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (-\infty; 0)$ и $x \in (0; +\infty)$;
$y < 0$ — нет.

функция возрастает на $[0; +\infty)$;
функция убывает на $(-\infty; 0]$.

г) $y = \sqrt{x}$;

$y_{\text{наиб}}$ — не существует; $y_{\text{наим}} = 0$.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (0; +\infty)$;
$y < 0$ — нет.

функция возрастает на $[0; +\infty)$.

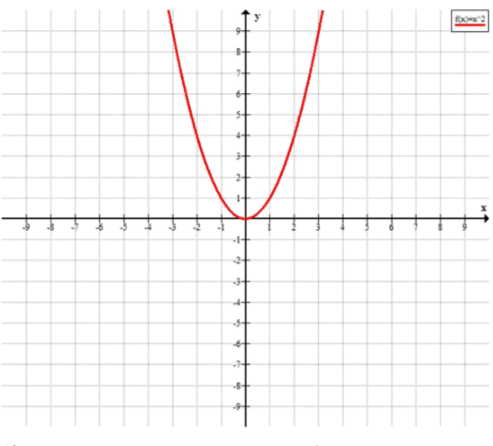
а) Рассмотрим функцию $y = x^2$. Для анализа её поведения и нахождения значений, которые эта функция может принимать, рассмотрим все основные моменты, такие как наибольшее и наименьшее значения функции, пересечения с осями, интервалы возрастания и убывания.

Найдем наибольшее и наименьшее значения функции.
Функция $y = x^2$ является параболой, которая открывается вверх, поскольку коэффициент при $x^2$ положительный. Вершина этой параболы — это точка $(0; 0)$, где достигается минимальное значение. Это связано с тем, что квадрат любого числа не может быть отрицательным, а при $x = 0$ функция принимает наименьшее значение, равное 0. Поэтому наибольшее значение функции не существует, так как парабола стремится к бесконечности по мере увеличения $x$. Значение $y_{\text{наим}} = 0$ при $x = 0$, и это является минимальным значением функции.

Найдем точки пересечения функции с осью $x$.
Для того чтобы найти нули функции, приравняем её к нулю:

$$x^2 = 0$$

Решение этого уравнения очевидно: $x = 0$.

Таким образом, график функции пересекает ось $x$ в точке $(0; 0)$.

Рассмотрим знак функции на различных интервалах.
Так как функция $y = x^2$ всегда положительна для всех значений $x$ кроме нуля, то:

$y > 0$ при $x \in (-\infty; 0)$ и $x \in (0; +\infty)$,

$y < 0$ — нет, так как функция всегда неотрицательна.

Рассмотрим интервалы возрастания и убывания.
Для анализа монотонности функции найдем её производную:

$$f'(x) = 2x$$

• Если $x > 0$, то производная положительна, и функция возрастает.
• Если $x < 0$, то производная отрицательна, и функция убывает.
• В точке $x = 0$ производная равна нулю, что указывает на точку минимума.

Таким образом, функция возрастает на интервале $[0; +\infty)$ и убывает на интервале $(-\infty; 0]$.

Ответ:

$y_{\text{наиб}}$ — не существует; $y_{\text{наим}} = 0$.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (-\infty; 0)$ и $x \in (0; +\infty)$;
$y < 0$ — нет.

функция возрастает на $[0; +\infty)$,
функция убывает на $(-\infty; 0]$.

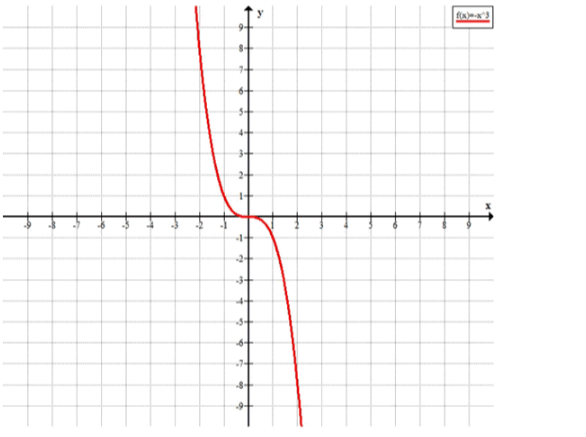
б) Рассмотрим функцию $y = -x^3$. Чтобы найти её нули, приравняем функцию к нулю:

$$-x^3 = 0$$

Решение этого уравнения даёт:

$$x = 0$$

Таким образом, функция пересекает ось $x$ в точке $(0; 0)$.

Теперь рассмотрим поведение функции на интервалах:

• При $x < 0$, функция принимает положительные значения, так как куб отрицательного числа также отрицателен, а перед числом стоит знак минус.
• При $x > 0$, функция принимает отрицательные значения, так как куб положительного числа остаётся положительным, а знак перед числом отрицательный.

Функция не имеет максимума или минимума, так как её значения продолжают уменьшаться или увеличиваться, не ограничиваясь.

Производная функции:

$$f'(x) = -3x^2$$

• При $x < 0$, производная положительна, и функция возрастает.
• При $x > 0$, производная отрицательна, и функция убывает.

Ответ:

$y_{\text{наиб}}$ и $y_{\text{наим}}$ — не существуют.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (-\infty; 0)$;
$y < 0$ при $x \in (0; +\infty)$.

функция убывает на $(-\infty; +\infty)$.

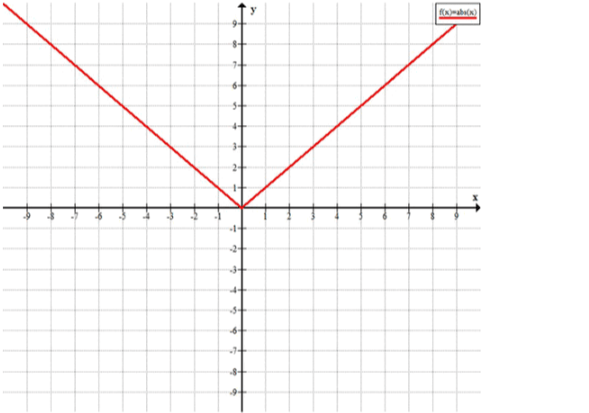
в) Рассмотрим функцию $y = |x|$. Для нахождения нулей функции приравняем её к нулю:

$$|x| = 0$$

Решение этого уравнения даёт:

$$x = 0$$

Таким образом, график функции пересекает ось $x$ в точке $(0; 0)$.

Теперь рассмотрим знаки функции на различных интервалах:

• При $x > 0$, функция $|x| = x$, то есть она положительна.
• При $x < 0$, функция $|x| = -x$, то есть она тоже положительна.
• Функция не может быть отрицательной, так как абсолютная величина любого числа не может быть меньше нуля.

Теперь рассмотрим производную функции:

$$f'(x) = \begin{cases} 1, & x > 0 \\ -1, & x < 0 \\ \end{cases}$$

• При $x > 0$, производная положительна, и функция возрастает.
• При $x < 0$, производная отрицательна, и функция убывает.

Ответ:

$y_{\text{наиб}}$ — не существует; $y_{\text{наим}} = 0$.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (-\infty; 0)$ и $x \in (0; +\infty)$;
$y < 0$ — нет.

функция возрастает на $[0; +\infty)$;
функция убывает на $(-\infty; 0]$.

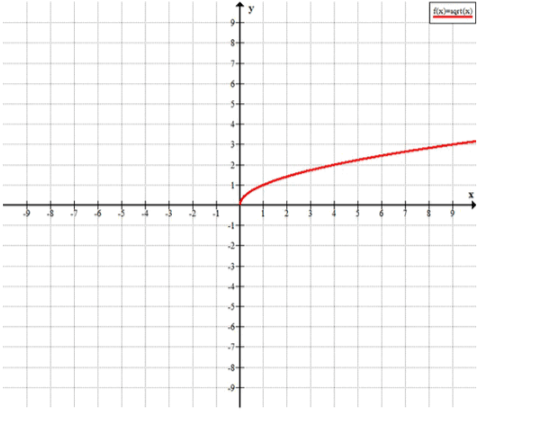
г) Рассмотрим функцию $y = \sqrt{x}$. Для того чтобы найти нули функции, приравняем её к нулю:

$$\sqrt{x} = 0$$

Решение этого уравнения даёт:

$$x = 0$$

Таким образом, график функции пересекает ось $x$ в точке $(0; 0)$.

Теперь рассмотрим поведение функции на интервалах:

• Для $x > 0$, функция $\sqrt{x}$ принимает положительные значения, так как корень из положительного числа всегда положителен.
• Для $x < 0$, функция не существует, так как корень из отрицательного числа не существует в области действительных чисел.

Производная функции:

$$f'(x) = \frac{1}{2\sqrt{x}}$$

• Для $x > 0$, производная положительна, и функция возрастает.

Ответ:

$y_{\text{наиб}}$ — не существует; $y_{\text{наим}} = 0$.

$f(x) = 0$ при $x = 0$.

$y > 0$ при $x \in (0; +\infty)$;
$y < 0$ — нет.

функция возрастает на $[0; +\infty)$.