Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 782 Дорофеев, Суворова — Подробные Ответы
Найдите нули функции:
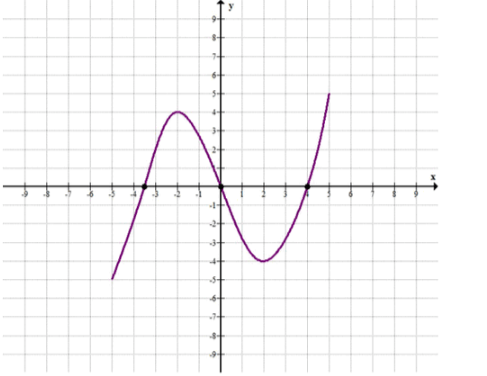
а) f(x)=(x-1)(x+3/2)(x-1/3);
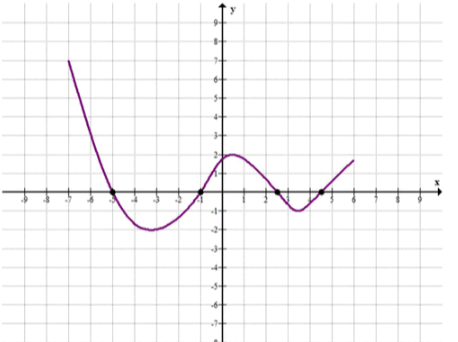
б) f(x)=x^2 (x+0,5)(2x-3);
в) f(x)=10x^4-250x^2;
г) y=3x^3-108x^2;
а) ; ; — нули функции;
; ; ;
при и ;
при и .
б) ; ; ; — нули функции;
; ; ; ;
при и и ;
при и .
а) Рассмотрим функцию , которая имеет нули в точках , , и . Мы знаем, что для функции, чьи графики пересекают ось в этих точках, значения при , , и равны нулю.
Чтобы найти интервалы, где и , необходимо рассмотреть знаки функции на промежутках, которые определяются этими нулями:
- При , подставляем в уравнение функции. Получаем, что , что подтверждает, что на этом интервале функция отрицательна.
- При , подставляем в уравнение функции. Получаем, что , что подтверждает, что на этом интервале функция положительна.
- При , подставляем в уравнение функции. Получаем, что , что подтверждает, что на этом интервале функция отрицательна.
- При , подставляем в уравнение функции. Получаем, что , что подтверждает, что на этом интервале функция положительна.
Таким образом, для интервалов:
- при и ,
- при и .
Ответ: , , — нули функции;
; ; ;
при и ;
при и .
б) Рассмотрим функцию , которая также имеет нули в точках. Для того чтобы найти нули этой функции, приравняем её к нулю:
Используем свойство произведения, что если произведение нескольких выражений равно нулю, то хотя бы одно из этих выражений должно быть равно нулю. Таким образом, решаем каждое из уравнений:
, даёт ,
, даёт ,
, даёт .
Значит, нули функции находятся при , , и .
Теперь рассмотрим знаки функции на промежутках, определённых этими нулями:
- При , подставляем . Получаем , что подтверждает, что функция положительна на этом интервале.
- При , подставляем . Получаем , что подтверждает, что функция отрицательна на этом интервале.
- При , подставляем . Получаем , что подтверждает, что функция положительна на этом интервале.
- При , подставляем . Получаем , что подтверждает, что функция положительна на этом интервале.
Таким образом, для интервалов:
- при , , , и ,
- при и .
Ответ:
, , .
Алгебра