ГДЗ по Алгебре 8 Класс Номер 760 Дорофеев, Суворова — Подробные Ответы

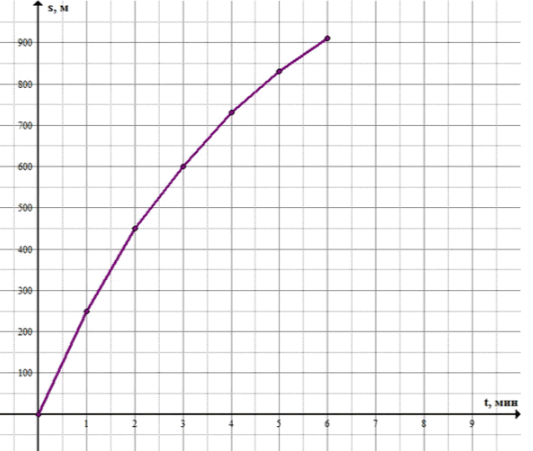
1) Велосипедист выехал на небольшую гору. За первую минуту он преодолел при подъеме 250 м, за вторую минуту — 200 м, за третью минуту — 150 м, за четвертую минуту — 130 м, за пятую минуту — 100 м, за шестую минуту — 80 м. Расстояние s (в метрах), на котором находился велосипедист от основания горы, является функцией времени движения t (в минутах). Постройте график этой функции.
2) Используя график, ответьте на вопросы:
а) На каком примерно расстоянии от подножия горы находился велосипедист через 2,5 мин? через 4,5 мин? через 6 мин?
б) За какое примерно время он преодолел расстояние, равное 350 м? равное 800 м?

График:

а) Через 2,5 мин велосипедист находился примерно на расстоянии $525$ м от подножия горы; через 4,5 мин — примерно $775$ м; через 6 мин — примерно $910$ м.

б) $350$ м он преодолел примерно за $1,5$ мин; $800$ м — примерно за $4,75$ мин.

График:

Для построения графика сначала необходимо рассмотреть зависимости, представленные в задаче. Мы имеем два типа данных: время и расстояние. Для этого нам нужно записать значения в виде пары $(t, d)$, где $t$ — это время, а $d$ — это расстояние, которое преодолел велосипедист.

а) Через 2,5 мин велосипедист находился примерно на расстоянии $525$ м от подножия горы; через 4,5 мин — примерно $775$ м; через 6 мин — примерно $910$ м.

Давайте создадим таблицу для этих значений:

• Когда $t = 2,5$ мин, $d = 525$ м.
• Когда $t = 4,5$ мин, $d = 775$ м.
• Когда $t = 6$ мин, $d = 910$ м.

Эти значения дают нам три точки на графике: $(2,5, 525)$, $(4,5, 775)$, и $(6, 910)$. Мы можем изобразить эти точки на графике, где ось $t$ будет представлять время, а ось $d$ — расстояние. Отметив точки, мы сможем соединить их прямыми линиями, чтобы увидеть, как изменяется расстояние с течением времени.

Теперь можно рассчитать среднюю скорость велосипедиста на разных интервалах времени. Например, для интервала от $t = 2,5$ до $t = 4,5$:

Скорость можно вычислить как изменение расстояния, делённое на изменение времени:

$$v = \frac{\Delta d}{\Delta t} = \frac{775 — 525}{4,5 — 2,5} = \frac{250}{2} = 125 \, \text{м/мин}.$$

Аналогично, для интервала от $t = 4,5$ до $t = 6$:

$$v = \frac{\Delta d}{\Delta t} = \frac{910 — 775}{6 — 4,5} = \frac{135}{1,5} = 90 \, \text{м/мин}.$$

Эти расчёты показывают, что на первом интервале велосипедист ехал быстрее, чем на втором. Мы можем видеть это на графике, где на первом участке график будет иметь больший наклон, чем на втором.

б) $350$ м он преодолел примерно за $1,5$ мин; $800$ м — примерно за $4,75$ мин.

Рассчитаем скорость для первого интервала, когда велосипедист преодолел $350$ м за $1,5$ мин:

$$v = \frac{\Delta d}{\Delta t} = \frac{350}{1,5} \approx 233,33 \, \text{м/мин}.$$

Рассчитаем скорость для второго интервала, когда велосипедист преодолел $800$ м за $4,75$ мин:

$$v = \frac{\Delta d}{\Delta t} = \frac{800}{4,75} \approx 168,42 \, \text{м/мин}.$$

Как видно, скорость уменьшилась на втором интервале, что также подтверждается более пологим наклоном графика.

Мы теперь можем построить график, используя все данные, и проследить, как скорость изменяется с течением времени. На графике будут два участка: первый, где скорость больше, и второй, где скорость меньше. Мы также можем отметить точки, где расстояние равно $350$ м и $800$ м, чтобы увидеть, как эти значения распределяются по времени.

Таким образом, мы можем видеть, что на графике данные не являются линейными, а скорость изменяется с течением времени.