ГДЗ по Алгебре 8 Класс Номер 759 Дорофеев, Суворова — Подробные Ответы

Маша посадила подсолнух и в течение 12 недель вела наблюдение за его ростом, измеряя длину стебля в конце каждой недели. Результаты ее наблюдений представлены в следующей таблице:
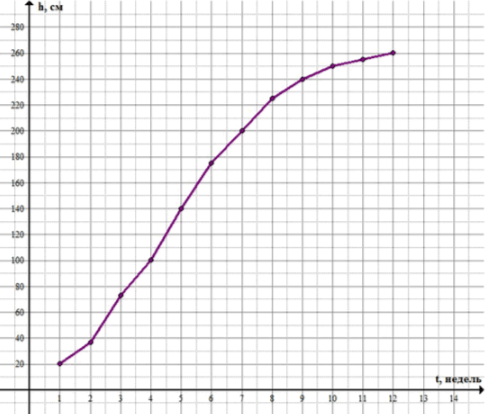
Постройте график функции h=f(t), где t — время (нед.), h — длина стебля (см). Используя график, ответьте на вопросы:
а) Какой примерно была длина стебля через 3,5 недели? через 6,5 недели?
б) Примерно на какой день длина стеля достигла 50 см; 210 см?
в) В какую неделю подсолнух рос быстрее всего, а в какую — медленнее всего?
г) Когда рост растений был интенсивнее — в первые четыре недели или в следующие четыре недели?
д) Когда подсолнух перерос Машу, если ее рост 152 см?

$h = f(t)$;

а) Через 3,5 недели длина стебля примерно была $85 \, \text{см}$; через 6,5 недели примерно — $190 \, \text{см}$.

б) Длина стебля достигла $50 \, \text{см}$ примерно на 17 день $(2,5 \cdot 7 = 17.5)$; длина стебля достигла $210 \, \text{см}$ примерно на 52 день $(7,5 \cdot 7 = 52.5)$.

в) Быстрее всего подсолнух рос с 4 по 5 неделю; медленнее всего — с 10 по 12 неделю.

г) Рост растения был интенсивнее с 5 по 8 неделю.

д) Подсолнух перерос Машу на 6 неделю.

$h = f(t)$;

Это математическое выражение указывает на то, что величина $h$ зависит от времени $t$. В данном контексте функция $f(t)$ может представлять рост растения во времени. То есть значение $h$ (например, длина стебля растения) изменяется в зависимости от времени $t$. Если $t$ — это время, то $f(t)$ указывает, сколько сантиметров длина стебля растения составляет в момент времени $t$. В зависимости от контекста функции $f(t)$ могут быть разными для разных растений, а также могут включать различные математические зависимости, такие как линейные, экспоненциальные или другие.

а) Через 3,5 недели длина стебля примерно была $85 \, \text{см}$; через 6,5 недели примерно — $190 \, \text{см}$.

Это утверждение говорит о том, как менялась длина стебля подсолнуха через определенные промежутки времени.

Через $3,5$ недели длина стебля была примерно $85 \, \text{см}$. Это значит, что в момент времени $t = 3,5$ недели значение функции $f(t)$ равно $85$, то есть $f(3,5) = 85$.

Через $6,5$ недели длина стебля была примерно $190 \, \text{см}$. Это значит, что в момент времени $t = 6,5$ недели значение функции $f(t)$ равно $190$, то есть $f(6,5) = 190$.

Эти данные можно использовать для анализа скорости роста растения в разные промежутки времени и для построения графика функции роста растения.

б) Длина стебля достигла $50 \, \text{см}$ примерно на 17 день $(2,5 \cdot 7 = 17.5)$; длина стебля достигла $210 \, \text{см}$ примерно на 52 день $(7,5 \cdot 7 = 52.5)$.

Здесь мы рассматриваем, когда длина стебля достигала определенных значений в днях.

Длина стебля достигла $50 \, \text{см}$ на 17-й день, что можно интерпретировать как $f(17) = 50$. Этот расчет использует, что $2,5 \cdot 7 = 17,5$, где $2,5$ — это число недель, а $7$ — количество дней в неделе, что дает в сумме 17,5, то есть на 17-й день.

Длина стебля достигла $210 \, \text{см}$ примерно на 52-й день, что можно записать как $f(52) = 210$. В этом случае $7,5 \cdot 7 = 52,5$, и это указывает на то, что длина стебля была равна $210 \, \text{см}$ на 52-й день.

Эти данные также могут быть использованы для вычисления скорости роста подсолнуха и для анализа, как быстро растение достигло этих размеров.

в) Быстрее всего подсолнух рос с 4 по 5 неделю; медленнее всего — с 10 по 12 неделю.

Это утверждение указывает на то, что рост растения не был равномерным и менялся в разные периоды времени.

С 4 по 5 неделю рост был наиболее интенсивным. Это означает, что в этот период времени скорость изменения длины стебля была наибольшей. График функции $f(t)$ в этот период будет иметь наибольший наклон. Это можно интерпретировать как более быстрый рост, что может быть связано с условиями окружающей среды или биологическими факторами, такими как поддержка уровня влажности или солнечного света.

С 10 по 12 неделю рост замедлился, что означает, что график функции $f(t)$ будет менее крутым в этот период, а прирост длины стебля будет меньшим, чем в другие недели.

г) Рост растения был интенсивнее с 5 по 8 неделю.

Этот промежуток времени указывает на то, что в интервале с 5 по 8 неделю рост растения был относительно быстрым. Это можно объяснить тем, что в этот период растения были в стадии активного роста. Функция роста $f(t)$ будет показывать более крутой наклон на графике в этом интервале времени. Возможно, это связано с оптимальными условиями для роста, такими как температура, влажность и доступность питательных веществ.

д) Подсолнух перерос Машу на 6 неделю.

Это означает, что к 6-й неделе рост подсолнуха стал быстрее, чем рост Маши, и в этот момент стебель подсолнуха стал длиннее, чем рост самой Маши. Графически это может быть представлено как точка пересечения функции роста подсолнуха с функцией роста Маши. Важно отметить, что такое явление часто встречается в наблюдениях за растениями, которые растут быстрее, чем животные или люди в условиях интенсивного роста.