ГДЗ по Алгебре 8 Класс Номер 758 Дорофеев, Суворова — Подробные Ответы

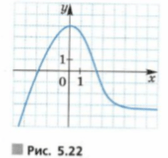
На рисунке 5.22 изображен график функции y=f(x). Найдите по этому графику:
а) f(0); f(-3); f(1);
б) значение x, при которых f(x)=2; f(x)=0; f(x)=-3.

$y = f(x)$;

$f(0) = 4$; $f(-3) = -0,5$; $f(1) = 3,5$;

$f(x) = 2, \quad x = -2, \quad x = 1,75$;

$f(x) = 0, \quad x = -2,75, \quad x = 2,5$;

$f(x) = -3, \quad x = -4, \quad x = 4,5$.

$y = f(x)$;

Это означает, что переменная $y$ зависит от переменной $x$. $f(x)$ — это функция, которая определяет, как для каждого значения $x$ вычисляется соответствующее значение $y$. Формально, можно записать это как функцию, где $y = f(x)$ для всех $x$, которые принадлежат области определения функции $f(x)$. Таким образом, $f(x)$ представляет собой закон, который отображает $x$ в $y$.

$f(0) = 4$; $f(-3) = -0,5$; $f(1) = 3,5$;

Здесь указаны конкретные значения функции $f(x)$ для некоторых значений $x$. Эти значения являются точками, которые удовлетворяют функции $f(x)$:

Для $x = 0$, функция $f(x)$ принимает значение $4$, то есть $f(0) = 4$.

Для $x = -3$, функция $f(x)$ принимает значение $-0,5$, то есть $f(-3) = -0,5$.

Для $x = 1$, функция $f(x)$ принимает значение $3,5$, то есть $f(1) = 3,5$.

Эти три значения дают нам три точки на графике функции. Мы можем использовать эти точки, чтобы построить график функции или найти закономерности в изменении функции на различных участках числовой оси.

$f(x) = 2, \quad x = -2, \quad x = 1,75$;

Это выражение говорит нам, что для значений $x = -2$ и $x = 1,75$, функция $f(x)$ принимает одинаковое значение $2$. Это означает, что функция $f(x)$ принимает одно и то же значение для двух разных значений $x$, что может означать наличие симметрии или определенных особенностей поведения функции на этих участках. На графике это будет выглядеть как две точки с одинаковым значением $y = 2$, но разными значениями $x$, что может указывать на экстремумы функции или симметричность графика.

$f(x) = 0, \quad x = -2,75, \quad x = 2,5$;

Здесь у нас снова две точки $x = -2,75$ и $x = 2,5$, для которых значение функции $f(x)$ равно 0. Это может быть важным моментом для анализа графика функции, так как такие значения показывают, где график функции пересекает ось $x$. В этих точках $y = 0$, и это может быть связано с корнями функции, то есть значениями $x$, при которых функция принимает нулевое значение.

$f(x) = -3, \quad x = -4, \quad x = 4,5$;

Здесь для двух значений $x = -4$ и $x = 4,5$, функция $f(x)$ принимает значение $-3$. Это снова два разных значения $x$, для которых функция имеет одинаковое значение $y = -3$. Такие точки могут говорить о наличии особых особенностей графика функции, например, о симметричности или о равенстве функции в разных точках числовой оси. На графике это будет две точки с одинаковым значением $y = -3$, но с различными значениями $x$.

Этот процесс и анализ данных точек функции помогает понять поведение функции в различных областях и на разных интервалах. Мы можем использовать такие данные для построения графиков, нахождения экстремумов функции, точек пересечения с осями и других характеристик, которые важны для понимания математической модели.