ГДЗ по Алгебре 8 Класс Номер 738 Дорофеев, Суворова — Подробные Ответы

а) Имелось 100 кг муки. Ежедневно расходовали 3 кг муки. Через x дней осталось y кг муки. Задайте формулой зависимость y от x. Найдите значение функции y при значении аргумента x, равном 3; 10; 33. Найдите значение аргумента, при котором значение функции равно 40; 55; 85. Укажите область определения функции.
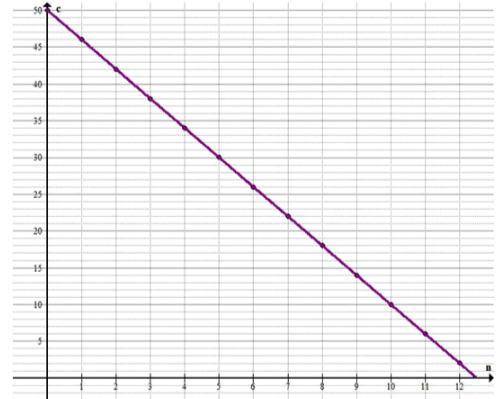
б) Нужно купить карандаши по 4 р. за штуку. Всего имеется 50 р. После покупки n карандашей останется c р. Задайте формулой зависимость c от n. Составьте таблицу значений аргумента n и функции c. Постройте соответствующие точки в координатной плоскости. Сколько точек получилось? Какова область определения функции?

а) $y = 100 — 3x$;
при $x = 3$:

$$y = 100 — 3 \cdot 3 = 91 \, (\text{кг}).$$

при $x = 10$:

$$y = 100 — 3 \cdot 10 = 70 \, (\text{кг}).$$

при $x = 33$:

$$y = 100 — 3 \cdot 33 = 1 \, (\text{кг}).$$

$3x = 100 — y$;

$$x = \frac{100 — y}{3}.$$

при $y = 40$:

$$x = \frac{100 — 40}{3} = 20 \, (\text{дней}).$$

при $y = 55$:

$$x = \frac{100 — 55}{3} = 15 \, (\text{дней}).$$

при $y = 85$:

$$x = \frac{100 — 85}{3} = 5 \, (\text{дней}).$$

Область определения функции: $0 \leq x \leq 33$,
$x$ — целое число.

б) $c = 50 — 4n$;

Построим точки:

Получилось 12 точек.

Область определения функции: $0 \leq n \leq 12$,
$n$ — целое число.

а) Задача с функцией $y = 100 — 3x$

У нас есть функция $y = 100 — 3x$, которая описывает зависимость между двумя переменными $x$ и $y$. Мы будем вычислять значение $y$ для различных значений $x$.

Шаг 1: Подставим значения $x$ в функцию $y = 100 — 3x$.

При $x = 3$:

$$y = 100 — 3 \cdot 3 = 100 — 9 = 91 \, (\text{кг}).$$

Это означает, что при $x = 3$, значение $y$ равно 91 кг.

При $x = 10$:

$$y = 100 — 3 \cdot 10 = 100 — 30 = 70 \, (\text{кг}).$$

Это означает, что при $x = 10$, значение $y$ равно 70 кг.

При $x = 33$:

$$y = 100 — 3 \cdot 33 = 100 — 99 = 1 \, (\text{кг}).$$

Это означает, что при $x = 33$, значение $y$ равно 1 кг.

Шаг 2: Теперь вычислим $x$, если известно значение $y$.

Для этого из уравнения $y = 100 — 3x$ выразим $x$:

$$3x = 100 — y$$ $$x = \frac{100 — y}{3}.$$

При $y = 40$:

$$x = \frac{100 — 40}{3} = \frac{60}{3} = 20 \, (\text{дней}).$$

При $y = 40$, значение $x$ равно 20 дней.

При $y = 55$:

$$x = \frac{100 — 55}{3} = \frac{45}{3} = 15 \, (\text{дней}).$$

При $y = 55$, значение $x$ равно 15 дней.

При $y = 85$:

$$x = \frac{100 — 85}{3} = \frac{15}{3} = 5 \, (\text{дней}).$$

При $y = 85$, значение $x$ равно 5 дней.

Шаг 3: Область определения функции.

• Функция $y = 100 — 3x$ имеет область определения $0 \leq x \leq 33$, так как при $x = 33$, значение $y = 1$, а при $x = 0$, значение $y = 100$.
• $x$ — целое число.

б) Задача с функцией $c = 50 — 4n$

Дана функция $c = 50 — 4n$, которая описывает зависимость между двумя переменными $n$ и $c$.

Шаг 1: Подставим различные значения $n$ в функцию $c = 50 — 4n$ и вычислим значения $c$.

Шаг 2: Построим точки.

Значения $c$ вычисляются с использованием функции $c = 50 — 4n$ для каждого значения $n$ от 0 до 12. Эти точки образуют последовательность значений, где с каждым увеличением $n$ на 1, $c$ уменьшается на 4.

Шаг 3: Область определения функции.

• В данном случае область определения функции — это значения $n$ от 0 до 12.
• $n$ — целое число, и для каждого $n$ мы вычисляем соответствующее значение $c$.

Ответ: Область определения функции: $0 \leq n \leq 12$, $n$ — целое число.