ГДЗ по Алгебре 8 Класс Номер 500 Дорофеев, Суворова — Подробные Ответы

На перекрестке двух дорог встретились пешеход и велосипедист, а затем каждый продолжил свой путь: велосипедист — на север со скоростью 12 км/ч, а пешеход — на восток со скоростью 5 км/ч. Через какое время после их встречи пешеход и велосипедист окажутся на расстоянии 26 км друг от друга?

Пусть через $x$ ч пешеход и велосипедист окажутся на расстоянии 26 км друг от друга.

Составим уравнение, используя теорему Пифагора:

$$(12x{)}^2+(5x{)}^2={26}^2$$

$$$$$$144x^2+25x^2=676$$

$$$$$$169x^2=676$$

$$$$$$x^2=4$$

$$$$$$x=2(\text{ч})\text{—между ними будет}26\text{км},$$

$$$$$$x=-2\text{—неподходит}\mathrm{.}$$

Ответ: через 2 ч.

Задано: Через $x$ часов пешеход и велосипедист окажутся на расстоянии 26 км друг от друга. Задача состоит в нахождении времени, через которое они будут на этом расстоянии. Для этого воспользуемся теоремой Пифагора.

Предположения:

• Пешеход идет со скоростью 12 км/ч, значит за $x$ часов он пройдет расстояние $12x$ км.
• Велосипедист едет со скоростью 5 км/ч, значит за $x$ часов он проедет расстояние $5x$ км.

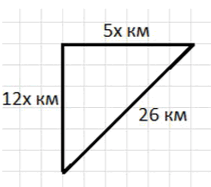
Таким образом, расстояние между ними через $x$ часов можно рассматривать как гипотенузу прямоугольного треугольника, где катеты — это расстояния, которые прошел пешеход и велосипедист.

Составление уравнения:
Применим теорему Пифагора для прямоугольного треугольника, где катеты — это расстояния, которые прошли пешеход и велосипедист, а гипотенуза — это расстояние между ними, которое равно 26 км:

$$(12x{)}^2+(5x{)}^2={26}^2$$

Это уравнение выражает зависимость между расстоянием, которое прошел пешеход, и расстоянием, которое проехал велосипедист, при условии, что между ними в итоге будет расстояние 26 км.

Раскрытие скобок:

$$144x^2+25x^2=676$$

Здесь мы раскрыли квадрат каждого из расстояний, получив два выражения с переменной $x^2$.

Суммирование одинаковых членов:

$$169x^2=676$$

Мы сложили $144x^2$ и $25x^2$, чтобы получить $169x^2$.

Решение уравнения:
Чтобы найти $x$, разделим обе части уравнения на 169:

$$x^2=\frac{676}{169}$$$$x^2=4$$

Извлечение квадратного корня:
Извлекаем квадратный корень из обеих сторон уравнения:

$$x=2(\text{ч})$$

Мы выбрали положительное значение, так как время не может быть отрицательным.

Проверка отрицательного значения:

$$x=-2\text{—неподходит}\mathrm{.}$$

Отрицательное значение не имеет смысла в контексте этой задачи, так как время не может быть отрицательным.

Ответ:
Пешеход и велосипедист будут на расстоянии 26 км друг от друга через 2 часа.

Ответ: через 2 ч.