ГДЗ по Алгебре 8 Класс Номер 480 Дорофеев, Суворова — Подробные Ответы

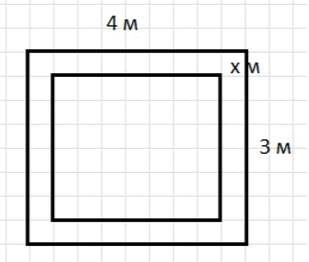
Витрина магазина имеет размер 3 х 4 м. При окраске здания на стекло по периметру витрины наклеили защитную бумажную ленту, чтобы не закрасить стекло. Лента закрыла площадь, равную половине площади витрины. Найдите ширину бумажной ленты.

Пусть $\mathrm{x }$м — ширина бумажной ленты, тогда размеры витрины равны

$4-2x$ м и $3-2\mathrm{x }$м.

Площадь витрины: $3\cdot 4=12{\text{м}}^2$.

А лента закрыла: $12:2=6{\text{м}}^2$.

Составим уравнение:

$$(4-2x)(3-2x)=6$$

$$12-8x-6x+4x^2-6=0$$

$$4x^2-14x+6=0\mathrm{\mid }:2$$

$$2x^2-7x+3=0$$

$$D=49-4\cdot 2\cdot 3=49-24=25=\sqrt{25}=5.$$

$$x_1=\frac{7-5}{4}=\frac{2}{4}=0,5(\text{м})\text{— ширина бумажной ленты};$$

$$x_2=\frac{7+5}{4}=\frac{12}{4}=3\text{— не подходит}\mathrm{.}$$

Ответ: $0,\mathrm{5 }$м.

1. Дано:

Пусть $\mathrm{x }$м — ширина бумажной ленты.

Тогда размеры витрины (с учетом ленты) равны

$4-2\mathrm{x }$м и $3-2\mathrm{x }$м.

Площадь витрины без ленты равна:

$$\text{Площадь витрины}=3\cdot 4=12{\text{м}}^2$$

Однако лента закрывает часть витрины. Площадь, которую закрыла лента, составляет:

$$\text{Площадь, закрытая лентой}=\frac{12}{2}=6{\text{м}}^2$$

Таким образом, площадь, оставшаяся для витрины после того, как лента её закрыла, составляет 6 м².

2. Составляем уравнение:

Площадь витрины с лентой можно выразить как произведение длин и ширин витрины с учетом ленты.

Размеры витрины с лентой составляют

$(4-2x)$м и $(3-2x)$м,

так как лента уменьшает оба размера витрины на $2\mathrm{x. }$

Итак, уравнение для площади витрины с лентой:

$$(4-2x)(3-2x)=6$$

3. Раскрываем скобки:

Теперь раскроем скобки в уравнении:

$$(4-2x)(3-2x)=4(3-2x)-2x(3-2x)$$

$$=12-8x-6x+4x^2$$

$$=12-14x+4x^2$$

Теперь подставим это в уравнение:

$$12-14x+4x^2=6$$

4. Переносим все на одну сторону:

Переносим 6 на левую сторону уравнения:

$$12-14x+4x^2-6=0$$

$$4x^2-14x+6=0$$

5. Делим на 2:

Чтобы упростить уравнение, поделим обе стороны на 2:

$$\frac{4x^2}{2}-\frac{14x}{2}+\frac{6}{2}=0$$

$$2x^2-7x+3=0$$

Теперь у нас квадратное уравнение:

$2x^2-7x+3=0$.

6. Находим дискриминант:

Для решения квадратного уравнения используем формулу дискриминанта:

$$D=b^2-4ac$$

где $a=2$, $b=-7$, $c=3$.

Подставляем значения:

$$D=(-7{)}^2-4\cdot 2\cdot 3=49-24=25$$

Таким образом, дискриминант $D=25$, и $\sqrt{25}=5$.

7. Находим корни уравнения:

Теперь находим корни уравнения с помощью формулы:

$$x=\frac{-b\pm \sqrt{D}}{2a}$$

Подставляем значения:

$$x=\frac{-(-7)\pm \sqrt{25}}{2\cdot 2}=\frac{7\pm 5}{4}$$

Таким образом, получаем два корня:

$$x_1=\frac{7-5}{4}=\frac{2}{4}=0,5(\text{м})\text{— ширина бумажной ленты}$$

$$x_2=\frac{7+5}{4}=\frac{12}{4}=3\text{— }$$

$$\text{не подходит, так как ширина ленты не может быть равна 3 м }$$

8. Ответ:

Ширина бумажной ленты составляет $0,\mathrm{5 }$м.

Ответ: $0,5$ м.